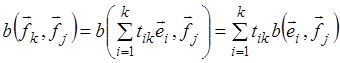Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 7

, следовательно, если (*) справедливо, то  ().

Используя линейность по второму аргументу, находим

 .

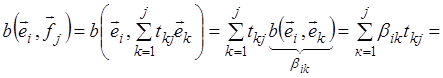
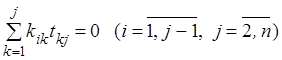Для каждого  запишем равенства (*) и получим систему линейных уравнений относительно  ().

.            (**)

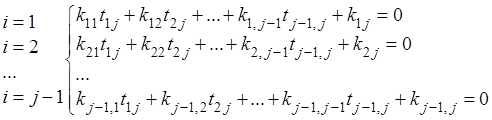Неизвестных коэффициентов здесь   () и столько же уравнений, причём определитель этой системы есть  (по условию теоремы). Следовательно, каждая система (при ) имеет единственное решение (теорема Крамера), т.е.  определяются однозначно.

Здесь можно в явном виде получить элементы  матрицы  и канонические коэффициенты .

Обозначим  минор матрицы , расположенный на пересечении строк с номерами  и столбцов с номерами , тогда, решая систему (**) по формулам Крамера найдём

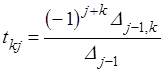  (,  )  .                          (7.8)

Найдём :

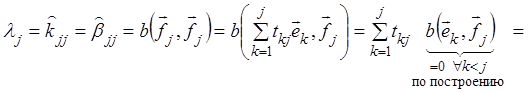
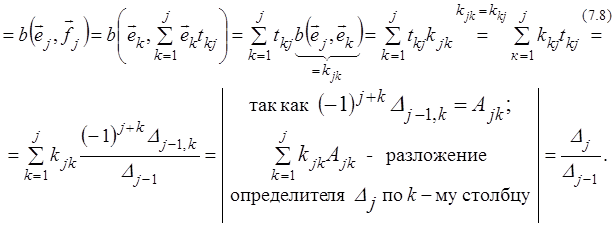
Таким образом,

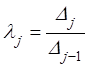 ();   .             (7.9)

Теорема 7.5. (Лагранжа) Любая квадратичная форма , заданная в п – мерном евклидовом пространстве , с помощью невырожденного линейного преобразования координат (базиса) может быть приведена к каноническому виду.

Доказательство (метод Лагранжа). Основная идея: дополнение многочлена до полного квадрата по каждому из аргументов.

Пусть в базисе

    и     такой, что .

С помощью невырожденного преобразования правую часть равенства можно преобразовать так, что коэффициент при квадрате первой координаты  вектора  будет отличен от нуля.

1) Если в данном базисе этот коэффициент отличен от нуля, то нужное преобразование является тождественным.

2) Если , но:

а) отличен от нуля коэффициент при квадрате какой-либо другой координаты, например, , тогда с помощью перенумерации базисных векторов  можно добиться требуемого результата. Перенумерация является невырожденным преобразованием, так как матрица перехода от одного базиса к другому имеет вид

  здесь detT = 1  0;

б) все , но тогда  (все нули быть не могут, так как в этом случае k()  0, что противоречит условию теоремы). Тогда нужное преобразование будет иметь вид

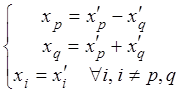  , матрица этого преобразования также невырожденная Х = ТХ', где

По теореме Лапласа (разложение по р-й и  q-й строкам)

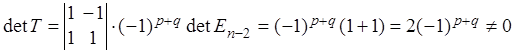, при этом

и далее см. а).

Итак, не ограничивая общности, можно сказать, что .

Выделим группу слагаемых, содержащих , т.е. представим форму в виде

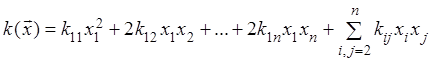
и дополним ее до полного квадрата, используя формулу

.

.

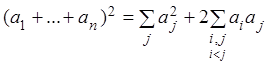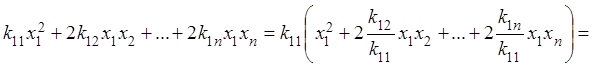
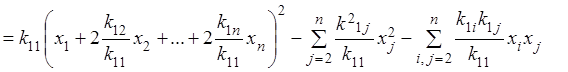Обозначая 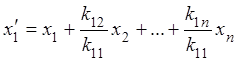, получим , где 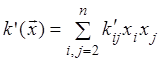 - квадратичная форма, не содержащая координаты , и коэффициенты этой квадратичной формы вычисляются по формулам:

 .

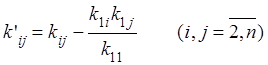Данное преобразование также является невырожденным

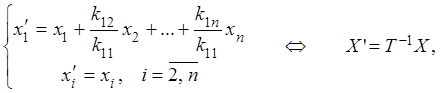   где

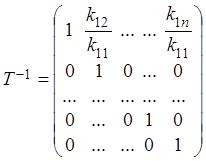, поэтому

(разложить по первому столбцу).

К квадратичной форме  можно применить тот же процесс и так далее, в результате на шаге с номером  получим канонический вид квадратичной формы. При этом матрица перехода к каноническому базису будет равна  – произведению невырожденных матриц и, следовательно, сама будет невырожденной.

Здесь  () – матрицы, рассмотренные выше.

7.3. Классификация квадратичных форм

Рассмотрим квадратичную форму

 .                                               (7.10)

Определение. Квадратичная форма  называется:

1)  положительно (отрицательно) определённой, если ,  выполняется неравенство

  ()  (знакоопределённые формы);

2)  неопределённой, если  для которых выполняются неравенства

,     (знакопеременные формы)

3)  полуопределённой, если  

  и для которого выполняется равенство .

Выявим условия, при которых имеет место каждая из этих ситуаций.

Замечание 1. Канонический базис определён неоднозначно (перенумеровывая базисные векторы будем получать различные канонические виды или см. метод Якоби).

Замечание 2. Если форма приведена к каноническому виду, то вообще говоря, не все коэффициенты  должны быть отличны от нуля. Оставим лишь ненулевые  и перенумеровывая переменные (базисные векторы) заново запишем

 .                                 (7.11)