Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 2

По определению , поэтому необходимо показать, что

.

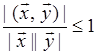Теорема 5.1. Для скалярного произведения в евклидовом пространстве  справедливо неравенство Коши-Буняковского

:   

или .

Доказательство. Рассмотрим функцию , где , из свойств 4, 5 скалярного произведения следует, что :  .

Применяя свойства 1, 2, 3, получим:

Так как :  ,  (свойство 4), то , где  – дискриминант квадратного трёхчлена, т.е. , следовательно

  или  .

Следствие 5.1. Из неравенства Коши-Буняковского получаем, что

  или 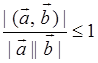 , следовательно, понятие угла определено корректно.

Определение. Векторы  и  называются перпендикулярными или ортогональными, если .

Будем считать, что вектор  ортогонален любому вектору.

Определение. Система векторов  в пространстве  называется ортогональной, если.

Определение. Система векторов в пространственазывается ортонормированной, если

    ,  где  – символ Кронекера.

Теорема 5.2. Любая ортонормированная система векторов в пространстве  линейно независима!

Доказательство. Пусть  – ортонормированная система векторов в . Рассмотрим равенство

                                        (*)

Умножим обе части равенства на  (), тогда

,

.

Так как  – ортогональны, то  при , следовательно , где  и :  .

Следовательно, равенство (*) возможно, если линейная комбинация тривиальна, это означает, что система векторов линейно независима.

Теорема 5.3. ВЕвклидовом пространстве  всегда существует ортонормированный базис!

Доказательство (метод математической индукции по размерности пространства п).

1) При п = 1 утверждение очевидно. Если  – ненулевой вектор, то вектор 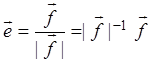 – ортонормированная система из одного вектора;

2) Предположим, что в каждом (п – 1) – мерном евклидовом пространстве существует ортонормированный базис  и покажем, что тогда утверждение верно и для п – мерного пространства.

Пусть  базис в пространстве  (вектор  – линейно независим с ). Линейная оболочка векторов  представляет собой(п – 1) – мерное евклидово пространство и по предположению индукции, там существует ортонормированная система из(п – 1) векторов . Рассмотрим вектор

                                                (**).

Коэффициенты  подберем так, чтобы вектор  былортогонален всем векторам. Умножим равенство (**) на векторы , получим

, откуда находим

     ().

Рассмотрим теперь вектор 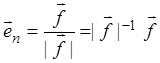. Длина его равна 1 и он ортогонален векторам , следовательно система векторов  ортонормированная и по теореме 5.2 образует базис в пространстве .

Метод, с помощью которого получен ортонормированный базис в пространстве  при доказательстве теоремы 5.3 называется методом ортогонализации.

Практическая реализация метода ортогонализации

Пусть  произвольный базис в пространстве .

1) Полагаем  (нормировать полученные векторы можно и потом).

2) Находим ортогональный базис в линейной оболочке векторов , полагаем , где  ,  тогда   и искомый базис .

3) Находим ортогональный базис в линейной оболочке векторов , полагаем , где 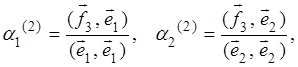  тогда  и искомый базис .

Повторяя эту процедуру, на п-м шаге получим ортогональный базис в . Нормируя каждый вектор, получаем ортонормированный базис.

Пример 5.1. Применить процесс ортогонализации к следующей системе векторов евклидова пространства:

.

Решение. Полагаем . Вектор  ищем в виде . Так как

 

(считаем, что векторы  заданы в ортонормированном базисе, который по теореме 5.3 всегда существует в ), то

.

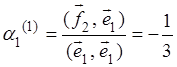Следовательно,

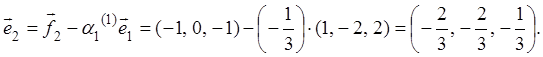
Наконец, вектор  находим в виде следующей линейной комбинации векторов:

.

Вычисляя скалярные произведения

,

находим значения коэффициентов:

  

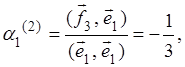
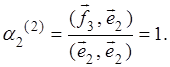
Следовательно,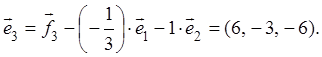

Таким образом, получаем следующую систему ортогональных векторов:

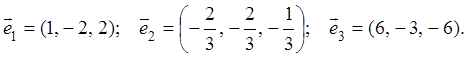
Разделив каждый вектор на его длину:

,  ,

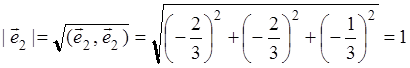, получим ортонормированный базис:

5.2. Выражение скалярного произведения векторов через координаты сомножителей

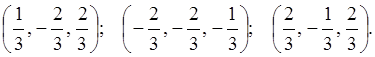
Пусть в  задан базис , значит :

тогда на основании свойств скалярного умножения

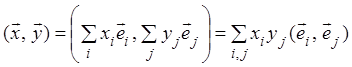                              (5.1)