Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 5

, , следовательно, , так как – произвольные векторы, то , следовательно, по определению – ортогональная матрица и .

Пример 6.1. Пусть линейный оператор , действующий в евклидовом пространстве, имеет в ортонормированном базисе матрицу . Построить в этом пространстве базис из собственных векторов оператора и найти матрицу оператора в этом базисе.

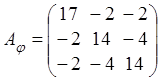Решение. 1) Найдем собственные числа оператора , для чего составим и решим характеристическое уравнение (4.3):

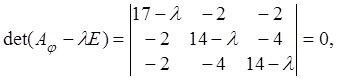
Приравняв к нулю, находим:

2) Находим собственные векторы, соответствующие найденным собственным значениям, для чего при каждом составляем и решаем систему (4.2): а) при , получаем

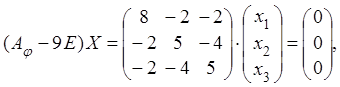
что равносильно системе (здесь )

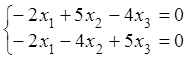, полагая в которой, например, , находим , таким образом, собственный вектор, соответствующий собственному значению 9, есть

б) при , получаем

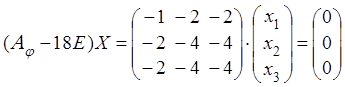
что равносильно уравнению (здесь )

, полагая в котором сначала , а затем , получаем еще два линейно независимых собственных вектора:

3) Находим матрицу перехода к базису из собственных векторов и обратную к ней (столбцами матрицы перехода являются координатные столбцы векторов (см. раздел 1)):

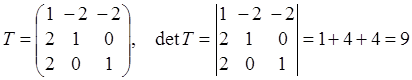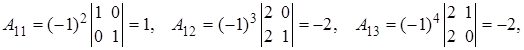
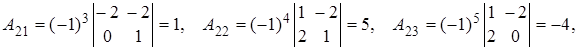
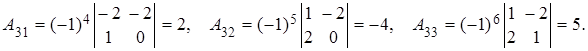
4) Теперь по формуле (4.1) находим – матрицу линейного оператора в базисе из собственных векторов

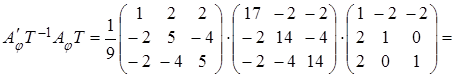
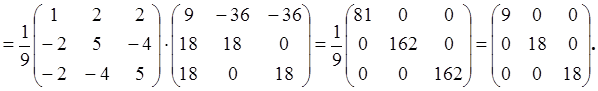
Таким образом, матрица линейного оператора в базисе из собственных векторов диагональная!

7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ

7.1. Билинейные формы

Определение. Отображение называется числовой функцией, т.е. числовая функция – закон или правило, по которому каждому вектору (каждой паре векторов ) ставится в соответствие число из R.

Определение. Числовая функция называется линейной формой,если и справедливо:

Определение. Числовая функция двух аргументов – закон или правило, по которому каждой паре векторов ставится в соответствие число из .

Определение. Числовая функция , аргументами которой являются всевозможные векторы , называется билинейной формой, если и выполняются соотношения:

а)

б)

в)

г)

т.е. функция является линейной по каждому из аргументов, где условия а), в) означают линейность по первому аргументу; условия б), г) – по второму.

Выберем какой - либо базис в . Тогда

и значение билинейной формы может быть вычислено следующим образом

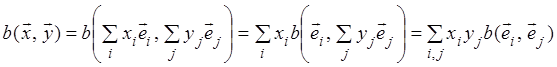
или

(7.1)

где (i, j = l, 2, ..., n) – значения билинейной формы на всевозможных парах базисных векторов, которые называются коэффициентами билинейной формы в базисе е.

Коэффициенты образуют квадратную матрицу порядка п

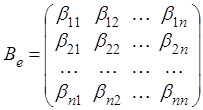, которая называется матрицей билинейной формы в данном базисе е. Как легко проверить, в матричном виде равенство (7.1) имеет вид

(7.2)

Теорема 7.1. Любая квадратная матрица в некотором базисе является матрицей билинейной формы.

Доказательство. Определим с базисом с помощью матрицы числовую функцию по правилу

Легко проверяются свойства (7.1). Но тогда элементы равны , где , и записанная формула есть определение билинейной формы (7.2).

Согласно теореме 7.1., естественно называть представление (7.2.) общим видом билинейной формы в n-мерном линейном Евклидовом пространстве .

Определение. Билинейная форма называется симметричной (кососимметричной), если выполняется равенство

Теорема 7.2. Билинейная форма является симметричной (кососимметричной) тогда и только тогда, когда ее матрица симметрическая, т.е. или (кососимметрическая, т.е. или ).