Неопределенный интеграл. Первообразная и неопределенный интеграл. Интегрирование некоторых иррациональных функций

числу весьма эффективных методов интегрирования относится метод интегрирования по частям.

Пусть функции u(х) и v(x) непрерывны на некотором промежутке и дифференцируемы во всех его внутренних точках, тогда, если на этом промежутке существует интеграл , то существует и интеграл , причем

    или      , эта формула называется формулой интегрирования по частям. Ее применение целесообразно в тех случаях, когда подынтегральное выражение  удается представить в виде произведения двух сомножителей u и dv таким образом, чтобы интегрирование выражений dv и vdu являлось задачей более простой, чем интегрирование исходного выражения.

Иногда для вычисления интеграла формула интегрирования по частям применяется несколько раз.

Укажем некоторые часто встречающиеся интегралы, которые вычисляются методом интегрирования по частям.

1) Интегралы вида

 

где  – многочлен n-ой степени, k = const, берутся по частям, если положить           u =  (после каждого интегрирования по частям степень многочлена понижается на единицу).

2) В интегралах вида

 за u при интегрировании по частям принимают функцию, являющуюся множителем при .

3) Интегралы вида

где a, b = const, находятся двукратным интегрированием по частям.

Пример 2.10. Найти интеграл

Решение.

Пример 2.11. Найти интеграл

Решение. Пусть   тогда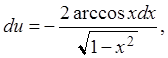   

и по формуле интегрирования по частям получаем

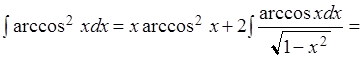
еще раз по формуле ,   

,

=

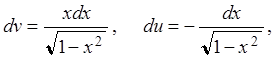
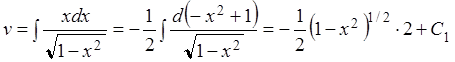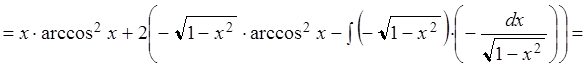
Пример 2.12. Вычислить

Решение. Обозначим

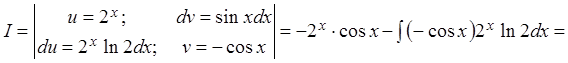
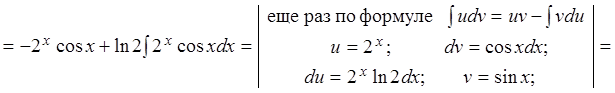
отсюда, выражая I,получим:

 

2.8. Интегрирование рациональных дробей

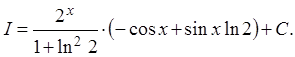
Определение. Дробь вида 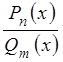, где  и  – многочлены n-ой и m-ой степеней соответственно, называется рациональной дробью.

Определение. Рациональная дробь называется правильной, если  и неправильной, если .

Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби, поделив числитель на знаменатель. Поэтому интегрирование рациональных дробей сводится к интегрированию правильных рациональных дробей. А каждая правильная рациональная дробь представима в виде элементарных (простейших) рациональных дробей, т.е. дробей вида

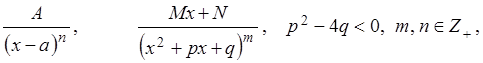
а их интегрирование производится следующим образом:

1) 

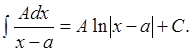
2)  .

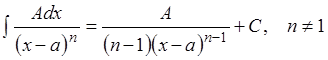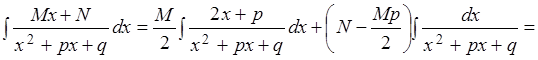
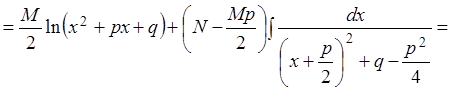
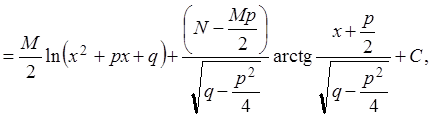
т.е. интеграл от элементарной рациональной дроби выражается через рациональные функции, логарифмы и арктангенсы.

Пример 2.13. Вычислить интеграл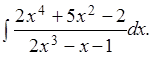

Решение. Подынтегральная функция – неправильная рациональная дробь.

Разделим многочлен  на многочлен

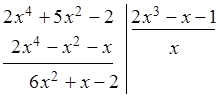
получим частное  и остаток , т.е. данная дробь представима в виде многочлена и правильной рациональной дроби:

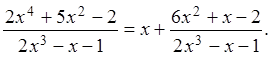
Разложим многочлен  на множители. Он имеет действительный корень . Разделив  на , получим

Квадратный трехчлен  не имеет действительных корней, поэтому разложение, полученной правильной рациональной дроби, на элементарные дроби имеет вид

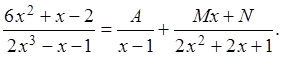
Методом неопределенных коэффициентов найдем А, М, N. Из равенства дробей следует равенство числителей

, а многочлены равны, когда равны коэффициенты при одинаковых степенях

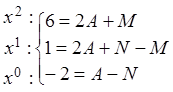
Решая систему, найдем  таким образом

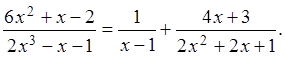
и, следовательно,

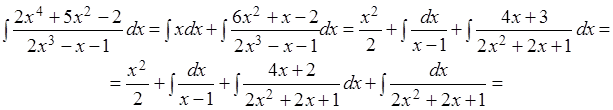
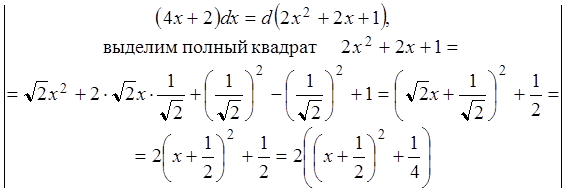
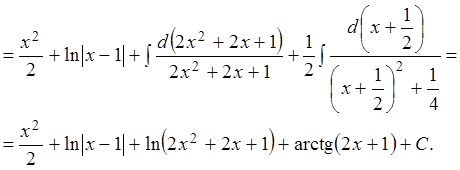
Пример 2.14. Вычислить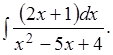

Решение. Разложим на простейшие дроби подынтегральную функцию, так как  то 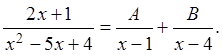 Методом неопределенных коэффициентов найдем А и В

.

Пусть , тогда  пусть  тогда

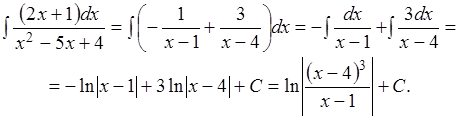
Пример 2.15. Вычислить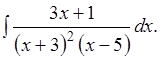

Решение. Знаменатель имеет двукратный корень  и простой корень  В этом случае разложение подынтегральной функции на простейшие дроби имеет вид

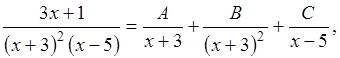
откуда       или

сравнивая коэффициенты при одинаковых степенях х, получим систему

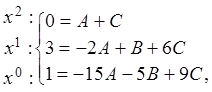
откуда находим 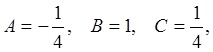 следовательно

2.9. Интегрирование некоторых тригонометрических функций и выражений

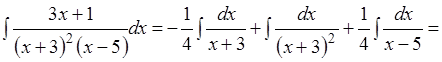
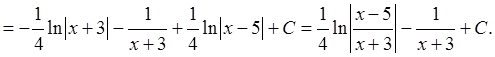
При вычислении интегралов вида  от четной степени синуса или косинуса используются формулы понижения степени

     

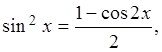
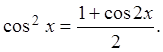
При вычислении интегралов вида       от нечетной степени синуса или косинуса нужно представить

        

и ввести новую переменную  в первом и  – во втором интегралах.

При вычислении интегралов вида

применяют формулы

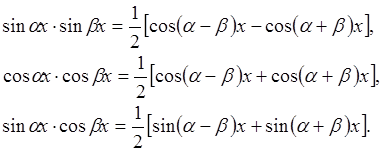
Пример 2.16. Найти

Решение.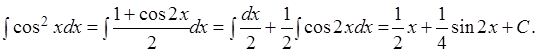

Пример 2.17. Вычислить

Решение.  

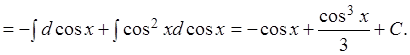
Рассмотрим интеграл вида  где  – рациональная функция переменных u и v, его всегда можно свести к интегралам от рациональных функций с помощью подстановки  (эта подстановка называется универсальной тригонометрической).

Так как 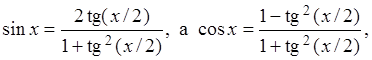   то

  

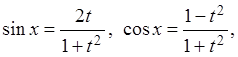
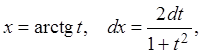
тогда

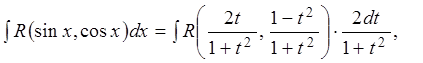
где под интегралом рациональная функция аргумента t.

Пример 2.18. Вычислить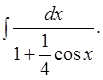

Решение. Применяя универсальную подстановку, получим

2.10. Интегрирование некоторых иррациональных функций

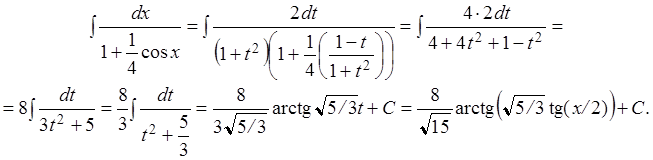
Рассмотрим интегралы вида

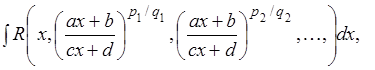
где R – рациональная функция;  – целые числа;а, b, с, d – некоторые постоянные.

Функция такого вида называется дробно-линейной иррациональностью