Скорость звука в различных средах. Волновое уравнение, его решения для плоской волны, волновое число, удельное акустическое сопротивление. Испарение капель в неподвижном газе, не содержащем пара

8. Скорость звука в различных средах.

Звуковые волны - механические колебания в упругой среде. Распространение колебаний в среде описывается волновым уравнением  

                             ,

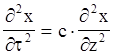где: x - перемещение частиц среды поперёк направлению распространения волны, z - перемещение вдоль волны, с - скорость распространения колебаний (скорость звука). Это уравнение справедливо для колебаний с малой амплитудой.

Кроме скорости звука колебания определяются: длиной волны , частотой колебаний f, периодом колебаний Т, и круговой частотой колебаний , которые вязаны между собой соотношениями:   ,  , . Скорость звука зависит от свойств среды, её термодинамических параметров и от частоты колебаний.

Скорость звука в различных средах определяется зависимостями:

  в газах                       ,     

 где:  - показатель адиабаты, R - газовая постоянная, Т - абсолютная температура газа;

в жидкостях: ,

где  - модуль объёмной упругости (модуль Юнга);

в твёрдой среде

 скорость распространения продольных колебаний в стержне

                                    

где Е - модуль упругости материала.

10.Волновое уравнение, его решения для плоской волны, волновое число, удельное акустическое сопротивление.

В зависимости от граничных условий существуют различные решения волнового уравнения. Для перемещения частиц среды в плоской волне решение волнового уравнения имеет вид:

                                 ;

для цилиндрической волны:

                                 ;

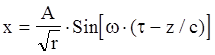для сферической волны:

                                  ;

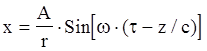здесь: А - амплитуда перемещения частиц,  - текущее время.

Решение волнового уравнения для перемещения частиц в плоской волне можно представить в виде:

                                 

где:    - волновое число.

Решение волнового уравнения для скорости перемещения частиц в плоской волне

                        

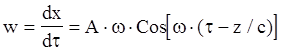
или                ,

где   - амплитуда скорости перемещения частиц.

Для давления среды в плоской волне:

         

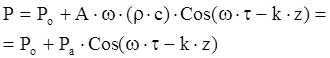
где:  - амплитуда давления, Р_о - начальное давление в спокойной среде,  - удельное акустическое сопротивление.

Следует помнить, что      и   .

11.Поглощение звука средой, коэффициент поглощения, глубина проникновения, время релаксации.

Любые колебания при распространении в реальной среде со временем затухают, так как энергия колебаний (волны) поглощается средой и в ней диссипирует, в конечном счёте, превращается в тепло, среда нагревается. Звук также поглощается средой, и интенсивность его падает по экспоненте:

,

здесь:  - коэффициент поглощения, обратная величина  - глубина проникновения.

Коэффициент поглощения   зависит от термодинамических параметров среды (давления, температуры), физических свойств среды и частоты излучения . Так, например, энергия звука при распространении в воде при частоте f = 40 кГц падает на одну треть через 30 км, а при частоте f = 100 кГц - уже через 5 км. Соответственно уменьшается амплитуда колебаний, так на расстоянии равном глубине проникновения   амплитуда волны уменьшается втрое: А = 0.37А_о. Так как коэффициент поглощения зависит от разных причин, считают, что он складывается из следующих составляющих:

где:  - вязкое (стоксовское) поглощение, обусловленное вязкостью среды ,      - поглощение за счёт теплопроводности среды,   -  диффузионное (объёмное) поглощение, или:  

                              ,

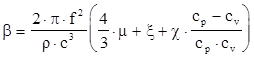где:  - коэффициент объёмного поглощения,  - показатель адиабаты.

Следует отметить, что     для любой среды. Максимальное поглощение происходит тогда, когда период колебаний Т равен времени релаксации Время релаксации - это время, за которое энергия волны уменьшается в раз.

Кроме того, за счёт различных механизмов поглощения акустическая волна искажается.

12. Основные характеристики звукового излучения

Сила (интенсивность) звука - энергия звуковых (акустических) волн, проходящая через единицу поверхности в единицу времени [вт/см²]:                                                .

Звуковое давление

                          

Амплитуда колебаний

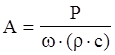
Уровень звука - относительная величина интенсивности звука к нормированному значению. За нормированную величину принят предел слышимости  J_o=10^-16 вт/см².

Уровень звука измеряется в децибелах (дБ). Например: сильную боль в ушах вызывает звук интенсивностью J=10^-2 вт/см², его уровень к = 140 дБ, уровень звука сильного шума соответствует к = 120 дБ, нормальная речь к = 60 дБ. В технологических процессах используют звук интенсивностью порядка      J = 10 вт/см².

13. Акустические воздействия