Скорость звука в различных средах. Волновое уравнение, его решения для плоской волны, волновое число, удельное акустическое сопротивление. Испарение капель в неподвижном газе, не содержащем пара, страница 20

При больших числах Рейнольдса наступает автомодельная область, где коэффициент сопротивлении становится постоянным .

Для малых частиц и в разреженных газах, когда размер частиц сравним со средней длиной свободного пробега молекул газа, на гравитационное осаждение накладывается броуновское движение за счёт ударов молекул газа. В этом случае вводят поправку Канингэма: 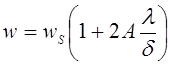, где - длина свободного пробега, - некоторая величина, которая для воздуха определяется как 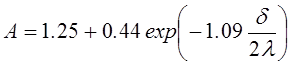. Для воздуха при нормальных условиях м. Длина свободного пробега увеличивается обратно пропорционально давлению. Для частиц крупнее 20 мкм поправка Канингэма мала.

В сдвиговом потоке (у стенки при движении аэрозоля в канале) на частицы действуют боковые силы, направленные перпендикулярно потоку, которые могут влиять на скорость осаждения частиц. В таком потоке возникает боковая сила Сафмана, направленная от стенки, величина которой 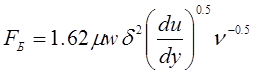. Эти силы существенны для малых частиц, соизмеримых с длиной свободного пробега. Для таких частиц в горизонтальном потоке у стенки при определении скорости осаждения, кроме поправки  Канингэма, вводят поправку на боковые силы: ,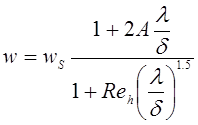

 где - число Рейнольдса для потока в канале.

На крупные частицы в сдвиговом потоке действуют боковые силы по направлению к стенке - силы Магнуса. Эти силы возникают из-за вращения частиц в сдвиговом потоке, их величина пропорциональна градиенту скорости потока у стенки, скорости движения частиц к стенке и кубу размера частиц: .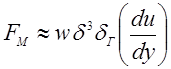

Приведённые выше формулы справедливы для шаровых частиц. Шаровую форму имеют частицы жидкости (туманы), твёрдые частицы обычно неправильной формы, что учитывают введением в выражения коэффициента формы, который можно найти в справочной литературе.

46.  Осаждение частиц в электрическом поле.

Осаждение в электрическом поле

Заряженные аэрозольные частицы в электрическом поле движутся к электродам и осаждаются на них. Для малых частиц, подчиняющихся закону сопротивления  Стокса, скорость движения заряженных частиц в электрическом поле:

,

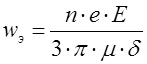здесь:  - число элементарных зарядов на частице,  - величина элементарного заряда (электрона),   - напряженность электрического поля.

Заряд частицы, приобретаемый в коронном разряде, можно оценить как:

,

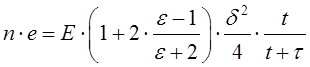здесь:  - диэлектрическая постоянная вещества частиц,  - время зарядки частицы,  - время, за которое частица приобретает половину предельного заряда.

Предельный заряд, который может приобрести частица:

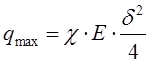.    Величина для большинства непроводящих частиц равна 1.5 – 2.0, а для проводящих – 3.0.

Если частицы менее 1 – 2 мкм, то заряд зависит от размера частиц линейно и в этом случае скорость движения частиц в электрическом поле не зависит от её размера:

.

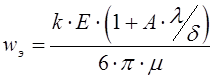Здесь  - поправка Канингема. Значение константы   лежит в пределах   и зависит от концентрации ионов и плотности тока у коронирующего электрода.

Свойство аэрозольных частиц двигаться в электрическом поле широко используется при очистке газов (электрофильтры).

47.  Термофорез.

Термофорез

Если в аэрозоле есть температурный градиент , то частицы движутся вдоль линий температурного поля в сторону понижения температуры. Термофоретические силы , действующие на частицу, существенно зависят от соотношения размера частиц и длины свободного пробега молекул газа. Для случая, когда размер частицы  больше длины свободного пробега , что соответствует высоким давлениям и крупным частицам, Эпштейн предложил зависимость:

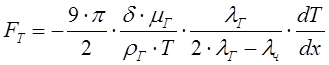             при  .

При , что соответствует низким давлениям и малым частицам,  термофоретические силы не зависят от теплопроводности  частиц и газа: 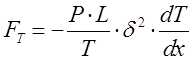                          , здесь  - давление газа.

Выражение для скорости движения частиц в поле градиента температур, полученное на основе молякулярно-кинетической теории:

              ,

откуда видно, что скорость термофореза пропорциональна градиенту температуры, обратно пропорциональна абсолютной температуре. Для малых частиц ()  скорость обратно пропорциональна давлению.