Очевидно, что в аэрозольном облаке одновременно идут
процессы испарения и конденсации частиц. Над поверхностью малых капель
парциальное давление паров ![]() больше, чем над
плоской поверхностью
больше, чем над
плоской поверхностью ![]() в соответствии с уравнением
Томсона- Гиббса
в соответствии с уравнением
Томсона- Гиббса 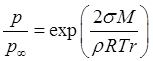 , в результате чего малые капли
будут испаряться в насыщенной среде, а на крупных каплях пар будет
конденсироваться. Это явление называют «изотермической перегонкой». На основе
этого Ленгмюр получил следующие выражения для полного времени жизни капель в
газе, насыщенном парами диспергированного вещества:
, в результате чего малые капли
будут испаряться в насыщенной среде, а на крупных каплях пар будет
конденсироваться. Это явление называют «изотермической перегонкой». На основе
этого Ленгмюр получил следующие выражения для полного времени жизни капель в
газе, насыщенном парами диспергированного вещества:
для ![]()
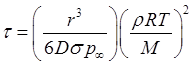 ,
(3.27а)
,
(3.27а)
для ![]()
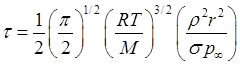 . (3.27б)
. (3.27б)
Как видно из этих соотношений, время жизни капель зависит от температуры. Так капли воды радиусом 1 мкм в воздухе, насыщенном водяным паром, полностью испаряются при температуре 20 0С за 0.6 секунд, а при температуре 0 0С – за 2 секунды.
Скорость испарения капель растворов может существенно отличаться от скорости испарения капель чистого растворителя. Растворы плохо растворимых веществ могут значительно увеличить время жизни капель. Так если к воде добавить 0.05 – 0.2 % цетилового спирта, образующего коллоидный раствор, время жизни капель может возрасти в сотни раз. Это происходит потому, что по мере испарения капли концентрация спирта на её поверхности сильно возрастает вследствие большого различия между скоростью диффузии молекул воды с поверхности капли во внешнюю среду и скоростью диффузии спирта от поверхности внутрь капли, в результате чего образуется монослой цетилового спирта, который медленно испаряется. Чем меньше капля, тем больше возрастает время её жизни в присутствии спирта. При радиусе капли 10 мкм время жизни возрастает почти в 250 раз.
Скорость испарения капли, покрытой плёнкой поверхностно-активного вещества, при некоторых условиях, может увеличиться вследствие увеличения коэффициента испарения.
50.Испарение капель в неподвижном газе, не содержащем пара.
Крупные капли под действием сил тяжести падают довольно быстро, и скорость их испарения при этом заметно возрастает. Определение скорости испарения капель, движущихся относительно газообразной среды, представляет интерес для многих технологических процессов: распылительная сушка, процессы в полых (распылительных) скрубберах, охлаждение распыленной водой, горение жидкого топлива, а также для метеорологии (испарение дождевых капель). Скорость испарения в этих условиях можно определить как
 ,
(3.24)
,
(3.24)
где ![]() - концентрация пара в
окружающем воздухе,
- концентрация пара в
окружающем воздухе, ![]() - константа, характеризующая
испаряющееся вещество,
- константа, характеризующая
испаряющееся вещество, ![]() - число Рейнольдса,
определённое по диаметру капли.
- число Рейнольдса,
определённое по диаметру капли.
При испарении капли охлаждаются на некоторую величину ![]() . Для неподвижной капли
. Для неподвижной капли
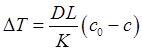 ,
(3.25)
,
(3.25)
здесь ![]() - удельная теплота
испарения,
- удельная теплота
испарения, ![]() - коэффициент теплопроводности воздуха.
Понижение температуры падающей испаряющейся капли будет зависеть от скорости
падения, соответственно от числа Рейнольдса
- коэффициент теплопроводности воздуха.
Понижение температуры падающей испаряющейся капли будет зависеть от скорости
падения, соответственно от числа Рейнольдса
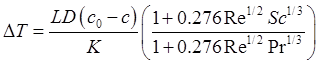 , (3.26)
, (3.26)
где  - число Рейнольдса,
- число Рейнольдса,  - число Шмидта,
- число Шмидта, 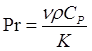 -
число Прандтля,
-
число Прандтля, ![]() - скорость капель относительно
воздуха,
- скорость капель относительно
воздуха, ![]() ,
, ![]() ,
, ![]() - кинематическая вязкость, плотность и
удельная теплоёмкость воздуха соответственно.
- кинематическая вязкость, плотность и
удельная теплоёмкость воздуха соответственно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.