Математическая логика и теория алгоритмов: Методические указания к практическим занятиям

Федеральное  агентство  по  образованию

Государственное  образовательное  учреждение

высшего  профессионального  образования

«Омский государственный технический университет»

МАТЕМАТИЧЕСКАЯ   ЛОГИКА  И  ТЕОРИЯ   АЛГОРИТМОВ

Методические   указания    к  практическим  занятиям

Омск – 2005

Составитель  Сечкина Ирина Викторовна, доцент, канд. пед. наук

Печатается по решению редакционно-издательского совета Омского государственного технического университета.

Основные  вопросы  данного курса разбиваются на три группы:

1. Алгебра высказываний; булевы функции;  релейно-контактные схемы.

2. Логические и кванторные операции  над предикатами; равносильность формул логики предикатов.

3. Представления об алгоритмах, машина Тьюринга; вычислительные алгоритмы.

Подобное разбиение  учебного материала осуществляется и на практических занятиях.

Главное внимание сосредоточено на усвоении важнейшего в математической логике понятия булевой алгебры и её основных моделей: алгебры  множеств, высказываний, событий и релейно-контактных схем.

Основные умения

1)  Равносильные преобразования формул алгебры высказываний и их представление совершенными формами;

2) Равносильные преобразования формул логики предикатов с помощью тавтологий, приведение формулы к приведенной форме;

3)  Описание и примеры работы машины Тьюринга;

4)  Конструирование релейно-контактных схем.

План практических  занятий

1. Алгебра Буля и её модели.

2. Представление булевых функций формулами. Сводка тавтологий. Совершенные формы.

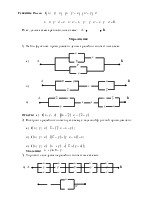
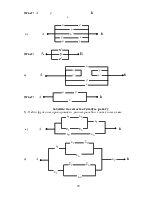
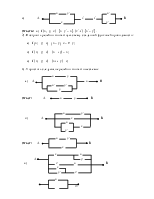
3.  Конструирование и упрощение релейно-контактных схем.

4.  Логические функции (предикаты) и операции над ними.

5.  Общезначимые формулы. Представление формул логики  предикатов в предваренной нормальной форме.

6.  Логика предикатов и алгебра множеств. Уравнения и неравенства как логические функции (предикаты). Комплекс теорем в геометрии. Необходимые и до-статочные условия.

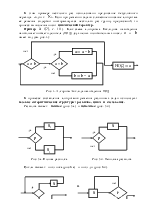
7.  Машина Тьюринга.

8.  Вычислительные алгоритмы.

9.  Контрольные мероприятия. Лабораторная работа.

Занятие 1. Алгебра Буля и её модели

Основоположником  формальной    (классической)   логики   считается  Аристотель – древнегреческий ученый (384-322 гг. до н. э.), а создателем мате-матической  логики  – Джордж  Буль - английский ученый  (1815-1864 гг.).

Разработанная Д. Булем алгебра названа в честь её автора булевой алгеброй, которая по своим свойствам отличается от обычной  алгебры чисел.

Определение 1. Алгеброй Буля  называется произвольное множество элементов    для которых  определены две операции – сложение и умножение, сопоставляющие каждым двум элементам     и    их сумму    и произведение  ; определена операция «черта», сопоставляющая каждому элементу     новый элемент     имеются два   «особых» элемента  0  и  1  и  вы-полняются следующие правила.

Коммутативные  законы

2)                    2а) 

Ассоциативные  законы

3)                                          3а)  

Идемпотентные законы

Правила, связывающие сложение и умножение:

4)                     4а)   .

Дистрибутивные  законы

Правила, относящиеся к элементам  0   и   1:

5)                                           5а)  

6)                                             6а)  

Правила, относящиеся к операции «черта»:

7) 

8)                                                  8а)  

Правила, связывающие операцию  «черта» со сложением и умножением:

9)                                     9а)      

Правила де Моргана

 Примеры алгебр Буля.

1) Алгебра двух чисел  «0»  и   «1»,  где операции  заданы  таблицей  «умножения»  и таблицей   «сложения»

Таблица  умножения                                                      Таблица   сложения

Заметим, что в этой алгебре   «1»+«1»=«1»,    а не  1 + 1 = 2, как в обычной алгебре чисел.

2) Алгебра максимумов и минимумов, где     означает взятие наибольшего числа из двух данных, а    означает взятие наименьшего числа из двух данных. Такое   «сложение»  и  «умножение»  можно задать таблицами:

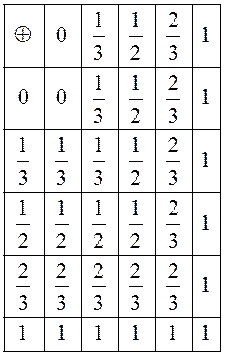
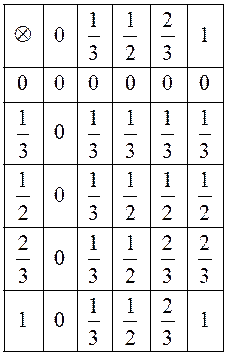
3) Алгебра наименьших общих кратных и наибольших  общих делителей двух чисел.

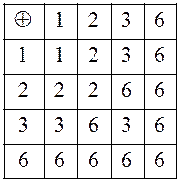
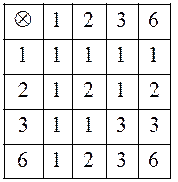
4) Алгебра множеств с операциями «сложения» (объединения), «умножения» (пересечение) и «черта» (дополнение).

5) Алгебра высказываний с операциями «сложения» (дизъюнкция), «умножения» (конъюнкция) и «черта» (отрицание).

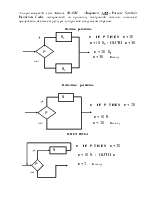
6) Алгебра контактных схем с операциями «сложения» (параллельное соединение контактов), «умножения» (последовательное  соединение контактов) и «черта» («замкнут» переводит в «разомкнут» и наоборот).

7) Алгебра событий  в теории вероятностей с операциями  «сложения» (сумма событий), «умножения» (произведение событий) и «черта» (противоположное событие).