Математическая логика и теория алгоритмов: Методические указания к практическим занятиям, страница 3

	закон двойного отрицания
	идемпотентность  конъюнкции
	идемпотентность  дизъюнкции
	коммутативность конъюнкции
	коммутативность  дизъюнкции
	ассоциативность конъюнкции
	ассоциативность  дизъюнкции
	дистрибутивность конъюнкции относительно дизъюнкции
	дистрибутивность  дизъюнкции относительно  конъюнкции
	законы поглощения
	законы де Моргана

      Определение 4. Конъюнктивным (дизъюнктивным) одночленом  от переменных    называется   конъюнкция (дизъюнкция) этих переменных или их отрицаний. Дизъюнктивной (конъюнктивной)  нормальной формой  называется произвольная дизъюнкция (конъюнкция) конъюнктивных (дизъюнктивных) одночленов.

Одночлен от переменных    называется совершенным, если каждая из этих переменных входит в него только один  раз со знаком отрицания или без знака  отрицания.

Нормальная форма  от переменных    называется  совершенной  (обозначается СДНФ  или  СКНФ), если  каждый входящий в эту форму одночлен является совершенным одночленом переменных  .

Определение 5.  Функцией  алгебры логики  называется всякая функция   принимающая значения  0  или  1  (истина  или  ложь), когда её пропозициональные переменные    (аргументы) принимают значения  0  или  1.

Кроме уже известных    по занятию 1 функций конъюнкция, дизъюнкция, импликация и эквиваленция, рассматривают функции:  штрих Шеффера  , стрелка Пирса    и  сумма    Жигалкина (сложение по модулю два), за данные таблицей истинности

           

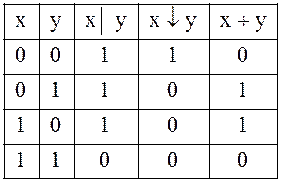
Определение 6. Система булевых функций    называется  полной,  если любая  функция алгебры логики есть суперпозиция функций системы   . 

Система булевых функций    называется  независимой,  если никакая функция    не представима суперпозицией  функций из подсистемы 

Система булевых функций из    называется  замкнутой,  если вместе с любыми функциями этой системы в нее входят и любые суперпозиции булевых  функций  системы.

Независимая система функций    называется  базисом  замкнутого класса булевых функций    если любая функция      есть суперпозиция функций  системы  .

Примеры.

1)           2)         3) 

4)   Следующие системы булевых функций является полными:

5)  Следующие системы булевых функций является неполными:

Упражнения.

1) Показать, что  

2) Выразить с помощью суперпозиций:

а)     через  

б)      через  

3)  Показать, что а)   (см. пример 1);

б) 

4)  Показать, что

a)    (см. пример 3);

б) 

в) 

г) 

д) 

5) Выразите  с  помощью  суперпозиций  булевы  функции  

   через стрелку  Пирса 

Задания на самостоятельную работу

1) Покажите, что        

        

где    сумма Жегалкина,      для всех 

2)  Построить таблицы истинности для  следующих булевых функций:

3) Выразить с помощью суперпозиций функции     через функции  

Чтобы привести формулу    не являющуюся тождественно ложной, к СДНФ, достаточно:

1)  привести её к какой-нибудь ДНФ;

2)  удалить члены дизъюнкции, содержащие переменную с её отрицанием;

3)  из одинаковых членов дизъюнкции оставить только один член;

4)  из одинаковых членов каждой конъюнкции удалить все, кроме одного члена;

5)  если в какой-нибудь конъюнкции нет переменной    из переменных, входящих в исходную формулу, то добавить к этой конъюнкции член     и применить дистрибутивный (распределительный) закон конъюнкции относительно дизъюнкции, затеи опять воспользоваться правилом 3)  по удалению одинаковых членов дизъюнкции.

Полученная формула будет  СДНФ.

Если данная формула    не является тавтологией (тождественно истинной), то её КНФ будет совершенной формой, т. е. будет СКНФ, если  выполнены следующие свойства:

1)  различны все члены конъюнкции;