Математика \ Математическая логика и теория алгоритмов

Математическая логика и теория алгоритмов: Методические указания к практическим занятиям, страница 9

Определение 14. Системой (совокупностью) двух уравнений называется конъюнкция (дизъюнкция) этих двух предикатов.

В соответствии с определением 14, множество истинности системы (совокупности) является пересечением (объединением) множеств истинности уравнений, входящих в систему (совокупность). Два уравнения называются несовместными, если пересечение их множеств истинности пусто.

Определение 15. Если в предикате (1) то уравнение (1) называется противоречивым. Если то уравнение (1) называется тождеством (на ).

Аналогично определяются уравнения с большим числом (предметных) переменных и неравенства:

(2)

с одним (предметным) переменным или несколькими переменными

Остановимся теперь на том, как пояснить общую схему нахождения решения уравнений, неравенств, их систем и совокупность: в основу нужно положить понятия логического следования и логической равносильности

Рассмотрим наиболее часто встречающиеся на практике равносильности:

I. Важные дизъюнкции

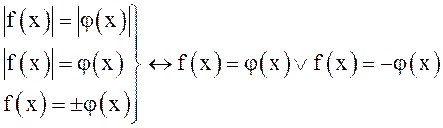
Здесь каждая логическая функция слева логически равносильна предикату справа.

8. 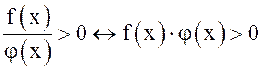(см. 2)

9. 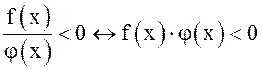(см.3)

10.

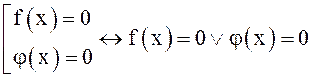
Здесь знак совокупности уравнений.

П. Важные конъюнкции

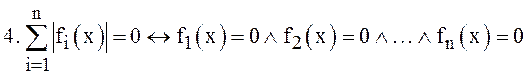
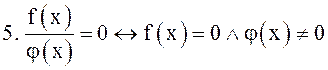
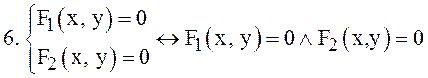
Здесь знак системы уравнений.

Примеры.

1. Решить уравнение

Исходное уравнение имеет вид оно эквивалентно совокупности двух систем:

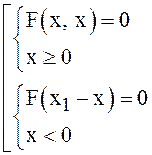Поэтому

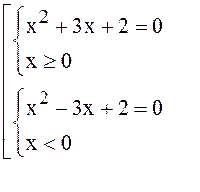
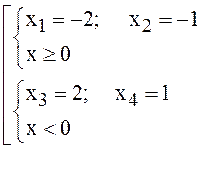
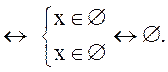
Ответ: (решений нет).

2. Решать неравенство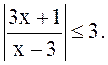

Решение. Данное неравенство равносильно системе

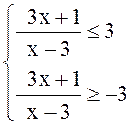
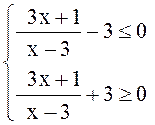
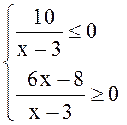
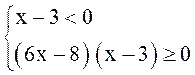
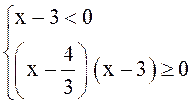
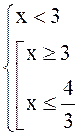
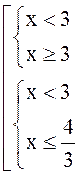
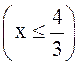Ответ: .

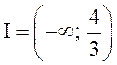Обратимся к изучению комплекса теорем. Для каждого предложения вида можно составить три предложения:

1) (обратное данному предложению ;

2) (противоположное данному);

3) (обратно-противоположное или противоположно-обратное).

Здесь называется условием, а заключением теоремы . По известному нам закону контрапозиции то есть вместо прямой теоремы можно доказать эквивалентную ей обратно-противоположную теорему .

Упражнения

1. Решить неравенство 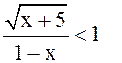([5], c. 207).

Ответ:

2. Решить неравенство 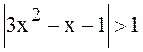([5], c. 179).

Ответ: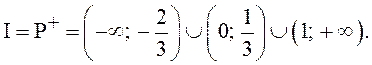

3. Решить уравнение

Указание. Использовать метод интервалов.

Ответ:

4. Решить уравнение 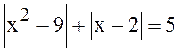методом интервалов.

Ответ: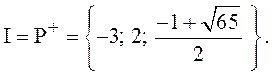

5. Решить уравнение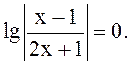

Ответ:

6. Решить уравнение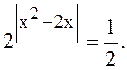

Ответ:

6. Пользуясь законом контрапозиции, доказать следующие теоремы:

а) Если нечетное число, то и нечетны.

б) Если значение выражения 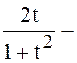иррациональное число, то –ирра-ционально. в) Если предложение является теоремой, то говорят, что есть

достаточное условие , а есть необходимое условие .

Теорему «Параллелограмм является ромбом тогда и только тогда, когда его диагонали перпендикулярны» сформулировать в виде необходимого и достаточного условия.

Упражнения на самостоятельную работу

1. Решить неравенство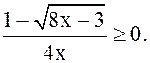

Ответ:

2. Решить неравенство

Ответ: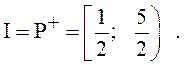

3. Решить уравнение

Ответ: то есть

4.Решить уравнение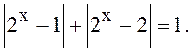

Указание. Использовать метод интервалов.

Ответ: т. е.

5. Для данных теорем сформулировать обратную теорему и теорему, равносильную данной по закону контрапозиции:

а) Если параллелограмм – ромб, то его диагонали взаимно перпендикулярны.

б) Если каждое слагаемое суммы чётно, то сумма чётна.

в) В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Какие из «обратных» теорем верны, а какие нет?

Занятие 7. Машина Тьюринга

Английский инженер и математик Алан Матисон Тьюринг (1912-1954) ввел понятие математической машины, моделирующей умственную деятельность человека и уточняющей интуитивное представление об алгоритмах.

Определение 15. Машина Тьюринга ([4], c.119) полностью определяется:

а) внешним алфавитом где символ пустой ячейки,