Математическая логика и теория алгоритмов: Методические указания к практическим занятиям, страница 7

                

      Ответы:                              -2 02 x

2)      или    т. е.       или      следовательно, 

3. Изобразить на координатной плоскости множества истинности следующих предикатов:

Ответ:  а)  Координаты любой точки четвертой четверти, включая её границу, обращают данный предикат в истинное высказывание. Следовательно, множество    совпадает со всей четвертой четвертью (см. рис. 1).

      

                                                    

                                                                                                                   

Рис. 1

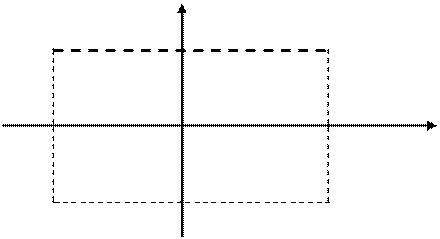
б)    совпадает с внутренней областью прямоугольника:

  (cм. рис. 1)

 

    2

3                    0                            3

-2

Рис. 2 

4. Определить является ли один из предикатов следствием другого, если они оба заданы  на  ¡:

      и    

     и     

       и        

Ответ:   б)       

¡:  Так как   ¡,  то предикат    является  следствием предиката  

5.  Из следующих предикатов с помощью навешивания кванторов и подстановки значений свободных переменных получить высказывания и определить их значения истинности:

Ответ: 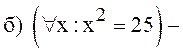 ложь;

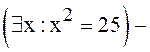истина.

истина;

ложь.

Занятие 5. Общезначимые формулы. Представление формул логики

предикатов в предваренной нормальной форме

В алфавит  символов, из которых конструируются формулы алгебры предикатов, входят:

1) предметные переменные 

2) нульместные предикатные переменные (высказывания);

3) местные   предикатные переменные 

4) символы логических операций: 

5) кванторы: 

6) вспомогательные  символы: скобка, запятая.

Определение 9.

1)  Каждая  нульместная предикатная переменная есть формула.

2)  Если  местная предикатная переменная, то   есть формула, в которой все предметные  переменные   являются  свободными переменными.

3)   Если  формула, то  также формула.

4)   Если      и   формулы, то    также формулы.

5)   Если  формула  со  свободной  переменной    ,  то     и      также  формулы со связанной переменной  .

6)   Никаких других формул логики предикатов, кроме перечисленных в пунктах 1–5, нет. Формулы, перечисленные в пунктах 1–2, называются  элементарными,  остальные – составными. Формулы, в которых нет свободных предметных переменных, называются  замкнутыми; формулы, содержащие свободные переменные, называются открытыми.

Определение 10. Формула логики предикатов называется  выполнимой  (опровержимой) на  множестве  ,  если при подстановке вместо предикатных переменных конкретных предикатов, заданных на   , она превращается  в выполнимый   (опровержимый) предикат. Формула логики предикатов называется  тождественно истинной (тождественно ложной)  на множестве  , если  при подстановке вместо предикатных переменных конкретных предикатов, заданных на  ,  она превращается в тождественно истинный (тождественно ложный) предикат.

Формула логики предикатов называется  общезначимой   или  тавтологией (тождественно ложной   или  противоречием), если при подстановке вместо предметных переменных любых предикатов, заданных на каких-угодно множествах, она  превращается в тождественно истинный (тождественно ложный) предикат.

Заметим, что в алгебре высказываний есть общий метод определения, является  или нет формула тавтологией – это составление таблиц истинности данной формулы, а в  логике  предикатов  такого   общего  метода  нет (это доказано в 1936 году

А. Чёрчем). Поэтому полезно знать основные равносильности  и основные тавтологии логики предикатов.

Определение 11. Формулы     и     логики предикатов называются равносильными на множестве    (просто  равносильными), если при подстановке в них вместо предикатных переменных любых  предикатов, определенных на множестве    (на любом множестве), формулы превращаются в равносильные предикаты. Обозначается   . Заметим, что    тогда и только тогда, когда     является тавтологией.

Основные равносильности логики предикатов

Основные тавтологии логики предикатов