Математическая логика и теория алгоритмов: Методические указания к практическим занятиям, страница 14

Пример 7. Программа генерирования членов последовательности

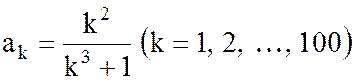
имеет вид ([8], c. 121).

1Ø   REM   

2Ø   REM   FOR-NEXT

3Ø   FOR      ТО   1 Ø Ø

4Ø  

5Ø    PRINT  

6Ø   NEXT    

Здесь тело цикла составляют строки   4Ø   и  5Ø, параметром цикла является переменная   , и выражение   STEP  в строке  3Ø  опущено.

Упражнения

1. Составить блок-схему и программу на Бейсике решения неравенства     где       и   – произвольные действительные числа.

Указание. См. рис. 53 и пример 4.3.2. из  [7], c. 166-167.

2.  Составить программу вычисления суммы всех членов ряда 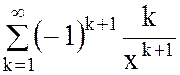 , не меньших по  абсолютной величине заданного числа 

Указание. См. рис. 55 и  пример  4.4.3    из  [7],  c. 171.

3. Составить программу табулирования функции 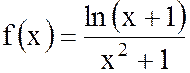    на отрезке  [0;  1]  c  шагом   0,05.

Указание.  См. пример 4.5.5  из  [8],c. 121.

Упражнения для самостоятельной работы

1. Составить блок-схему и программу на Бейсике решения квадратного уравнения     в области  действительных чисел.

Указание.  См. пример 3.4.2. из  [9], c. 131.

2. Составить блок-схему и программу  на Бейсике вычисления факториала     где  

Указание. См. пример  3.4.3.  из  [9],  c. 131-132.

3. Составить блок-схему и программу  на Бейсике вычисления членов последовательности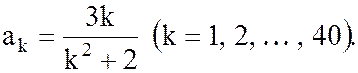   

4. Даны три числа     Составить блок-схему алгоритма, позволяющего определить, имеются ли среди них хотя бы одна пара взаимно обратных чисел.

Указание. См. рис. 49  и рис. 50  из  [9], c. 120-121.

5. Дан массив     Требуется определить,     имеется ли в этом массиве хотя бы одна пара взаимно обратных чисел.

Указание. См. пример 3.3.9. и рис. 51-53    из  [9], c. 121-122.

6.  Составить блок-схему поиска максимального  элемента в массиве  

Указание. См. пример 3.3.7. и рис. 27    из  [8], c. 91.

7. Составить блок-схему и программу  на Бейсике  решения задачи: имеется ли среди трех чисел      хотя бы одна пара равных между собой чисел.

8. Составить блок-схему и программу  на Бейсике  решения задачи: подсчитать количество отрицательных чисел среди чисел     и 

Занятие 9. Контрольные мероприятия. Лабораторная работа.

1.  Составив таблицу истинности, выяснить, равносильны ли следующие формулы алгебры высказываний:

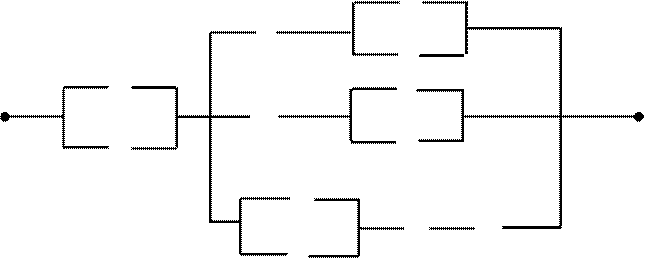
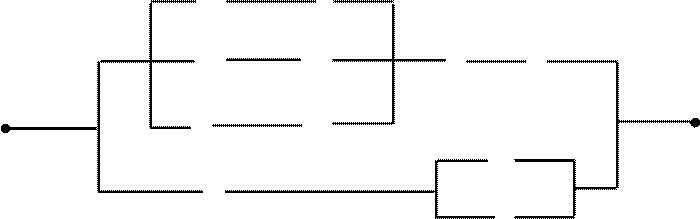
2. Упростить схему:

                                                               

                                              

                                              

          

Здесь    (отрицание  ).

3. Разложить предикат на простейшие функции и найти его множество истинности

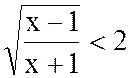    ([5], c. 172-173).

Вариант № 2

(Формулировка заданий в этом  и  последующих вариантах

 аналогична таковой варианта № 1)

1.

2.                                                     

                                            

                

3. 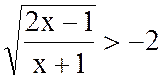         ([5], c.172).

Вариант № 3

1.   

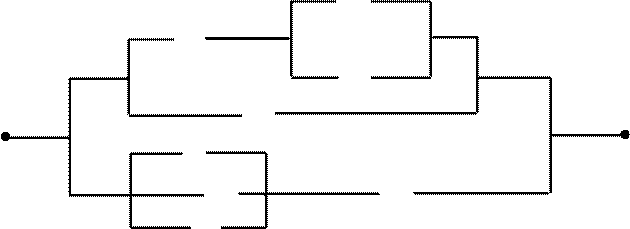2.                                                          

 

                        

3.             ([5], c.171).

Вариант № 4

1.   

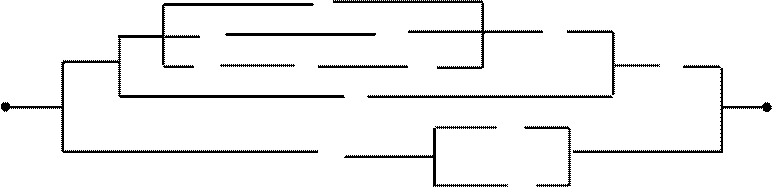2.                                           

                                                    

                                                                  

3.         ([5], c.174-175).

Вариант 5

1.   

2.

                                           

                            

        

                            

        

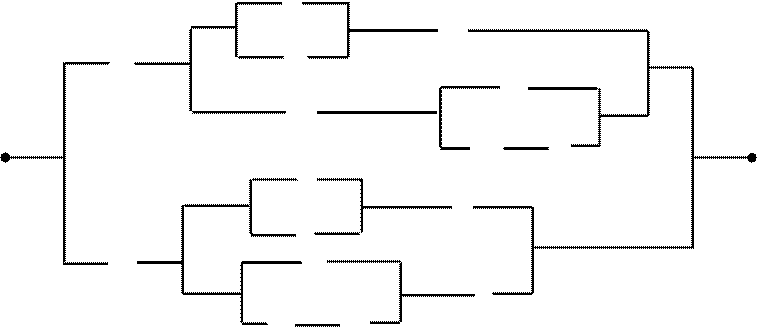
3.         ([5], c.175).

Типовой расчет

Вариант № 1

1.  Равносильными преобразованиями привести следующую формулу алгебры предикатов к предваренной нормальной форме ([4], c. 142).

2.  Машина Тьюринга с внешним алфавитом    определяется следующей программой  ([4], c. 125).

Остановится ли когда-нибудь эта машина, если она начнет перерабатывать данное слово    (в начальный момент в состоянии    машина  «обозревает»  ячейку, в которой записана самая левая буква данного слова).

Ответ:  Машина остановится; в результате получится исходное слово.

3.  Построив таблицы значений, выяснить, равны ли следующие булевы функции: