Математическая логика и теория алгоритмов: Методические указания к практическим занятиям, страница 2

Упражнения

1. Проверить выполнение аксиом алгебры  Буля  для  алгебр Буля из примеров

1) - 7).

2. Используя диаграммы Эйлера, показать справедливость правил де Моргана (1806-1871), английского математика, в теории множеств:

где  дополнение множества     до некоторого  универсального  множества 

3. Пусть дизъюнкция, конъюнкция, импликация и эквиваленция высказываний заданы таблицей истинности:

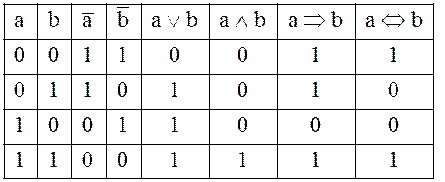
Здесь     и    – высказывания, т. е.  предложения, о которых можно судить: истинны они  или ложны (1  или  0),  дизъюнкция высказываний  

  и    (  или  );  конъюнкция  высказываний  (  и   );   импликация  (если  ,  то  ) и  эквиваленция  (  тогда и только тогда, когда   ),  отрицание      (не   ).

1)  Используя таблицу истинности, показать справедливость правил де Моргана:

2)  Используя операции  над высказываниями, дать определение а) объединения  и пересечения двух множеств;

б) суммы и произведения событий;

в) «суммы»  и  «произведения» двух контактов.

3) Построить контактную схему, отвечающую высказываниям:

a)  

б) 

в)  проверить  «равенство»   двух контактных схем

      и     .

Задания на самостоятельную работу

1. Составить таблицу «сложения» и   «умножения»  для алгебры  Буля из трех чисел 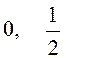 и     где      Проверить для этой алгебры выполнение аксиом алгебры Буля.

2. Проверить с помощью диаграммы Эйлера справедливость соотношения 

3. Сконструировать контактные  схемы, соответствующие высказываниям:

а) 

б) 

Занятие 2. Представление булевых функций формулами.

Сводка тавтологий. Совершенные  формы

Определение 2. Переменными высказываниями или  пропозициональными переменными  называются переменные    вместо которых можно подставлять высказывания (истинные или ложные). Формулы алгебры высказываний  определяются индуктивно: а) любая пропозициональная  переменная есть формула;

б) если     и     формулы алгебры высказываний, то    

   также  являются  формулами алгебры высказываний;

в) других формул алгебры высказываний, кроме формул, построенных по правилам   а)   и   б),  нет.

Формула      называется   выполнимой, если существует набор  высказываний      обращающий её  в истинное  высказывание. Формула     называется  тавтологией,  если она обращается в истинное  высказывание при всех наборах значений пропозициональных переменных  (обозначается   ).

Основные тавтологии алгебры высказываний

Определение 3. Формула     называется  логическим следствием  формул   , если  она обращается  в истинное высказывание на всяком наборе  значений переменных  для которого  все формулы    обращаются в истинные высказывания. Обозначают   

Формулы     и    называются  равносильными (эквивалентными), если при любых значениях переменных     значения истинности  высказываний, получающихся из формул  и   , совпадают. Обозначают  

Основные  равносильности  алгебры  высказываний