Математическая логика и теория алгоритмов: Методические указания к практическим занятиям, страница 11

Ответ:  б)       в) 

2.   Конструирование машин Тьюринга.

а)  Известно, что на ленте записано слово 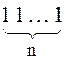   ,    Постройте машину Тьюринга с внешним алфавитом      которая отыскивала бы левую единицу этого слова и останавливалась, если  в начальный  момент головка машины  «обозревает»  одну из ячеек с буквой этого слова.

б) Постройте машину Тьюринга, которая бы к натуральному числу в десятичной системе счисления прибавляла единицу.

в) Дана конечная совокупность единиц, вписанных в ячейки, взятые подряд без пропусков. Постройте машину Тьюринга, которая записывала бы в десятичной системе число этих единиц.

Решение.   б) 

Начальное положение машины стандартное. Программу машины изобразим в виде функциональной схемы  ([4],c. 128).

      Ответы:  а) Программа машины:       

в)  Функциональная схема программы имеет следующий вид 

3.  Вычислимые по Тьюрингу  функции.

Докажите, что следующие функции вычислимы по Тьюрингу, для чего постройте машины Тьюринга, вычисляющие их:

а) 

Решение. Искомая машина Тьюринга определяется следующей функциональной схемой  ([4],c. 123):

Покажите, что следующие слова при начальном стандартном состоянии (  и «обозревает» крайнюю правую ячейку из тех, где записано слово) переводятся машиной в слова:

1)       в   

2)       в   

3)        в    

б) 

Ответ:  Машина Тьюринга определяется следующей функциональной схемой ([4], c. 124):

Убедитесь, что следующие слова машина  при начальном стандартном состоянии переведет в слова:

1)       в   

2)        в   

3)       в   

в)  Машина Тьюринга имеет следующую функциональную схему:

Найти формульное выражение функции     вычисляемое этой машиной.

Ответ: 

Упражнения для самостоятельной  работы

1. Дана машина Тьюринга с внешним алфавитом       алфавитом внутренних  состояний     и программой:

В какие слова переведёт машина из начального стандартного положения следующие слова:

а)                  б)                     

      Ответ:   a)                 б)                   в)  

2. Сконструируйте машину Тьюринга с внешним алфавитом      алфавитом  внутренних  состояний      которая каждое  слово  в алфавите    перерабатывает в пустое слово, исходя из стандартного начального состояния.