в)
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Ответ: ![]()
![]()
![]()
4). Составьте схему цепи с тремя независимыми контактами, которая замкнута тогда и только тогда, когда:
а) замкнута по меньшей мере два контакта;
б) замкнуты не более, чем два контакта;
в) разомкнут только один контакт.
Занятие 4. Логические функции (предикаты) и операции над ними
В традиционной логике в элементарном высказывании различаются субъект (то, что утверждается о субъекте), иначе говоря, подлежащее (субъект) и сказуемое (предикат). Предикат означает в этом случае свойство предмета.
В математической логике понятие предиката берется в более широком смысле как отношение между предметами, то есть предикат трактуется как логическая функция одной или нескольких предметных переменных.
Определение 8 [3]. ![]() местным
предикатом, определенным на
множествах
местным
предикатом, определенным на
множествах ![]() называется предложение, содержащее
называется предложение, содержащее ![]() переменных
переменных ![]() превращающееся
в высказывание при подстановке вместо этих переменных любых конкретных
элементов из множеств
превращающееся
в высказывание при подстановке вместо этих переменных любых конкретных
элементов из множеств ![]() собственно. Это
высказывание может быть либо истинным (предикат принимает значение 1), либо
ложным (предикат принимает значение 0). Если
собственно. Это
высказывание может быть либо истинным (предикат принимает значение 1), либо
ложным (предикат принимает значение 0). Если ![]() есть
область определения предиката
есть
область определения предиката ![]() то есть подмножество
то есть подмножество ![]() , на котором он обращается в истинное
высказывание, называется множеством истинности, то есть
, на котором он обращается в истинное
высказывание, называется множеством истинности, то есть
![]() .
.
Если 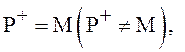 то предикат
то предикат ![]() называется
тождественно истинным ( опровержимым).
называется
тождественно истинным ( опровержимым).
Если 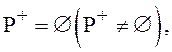 то предикат
то предикат ![]() называется
тождественно ложным (выполнимым).
называется
тождественно ложным (выполнимым).
Два предиката ![]() и называются равносильными,
если
и называются равносильными,
если ![]() Предикат
Предикат ![]() называется
следствием предиката
называется
следствием предиката ![]() , если
, если ![]() Обозначается:
Обозначается:
![]() и
и ![]() где
где ![]() знак равносильности,
знак равносильности, ![]() логическое следствие.
логическое следствие.
Над предикатами можно осуществлять те же логические операции, что и над высказываниями: отрицание, конъюнкцию, дизъюкнцию, импликацию, эквиваленцию и другие (известные нам) операции. При этом имеем
![]() (1)
(1)
![]() (2)
(2)
![]() , (3)
, (3)
где
![]() общая область определении предикатов
общая область определении предикатов ![]() и
и ![]() (формулы
(1) –(2)) или область определения предиката
(формулы
(1) –(2)) или область определения предиката ![]() (в
формуле (3));
(в
формуле (3));
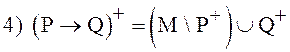 (4)
(4)
![]()
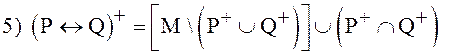 (5)
(5)
Логические операции преобразуют предикаты в предикаты. Рассмотрим теперь две операции, преобразующие предикаты в высказывания:
1) подстановка вместо всех предметных переменных их значений:
![]()
2) связывание всех переменных кванторами общности или существования;
3) подстановки вместо переменных, не связанных кванторами (то есть вместо свободных переменных), их значений – это комбинация первых двух операций.
Связанные переменные – это те переменные, которые фигурируют и в предикате,
и в кванторной записи типа ![]() и т.п., где
и т.п., где ![]() для всякого
для всякого ![]() квантор
всеобщности (общности), а
квантор
всеобщности (общности), а ![]() существует
существует ![]() квантор существования.
квантор существования.
Упражнения
1. Определить значение истинности следующих высказываний:
![]()
![]()
![]()
Ответ: а) истинное высказывание.
2. Найти множества истинности следующих предикатов и изобразить их на числовой прямой:
![]()
![]()
![]()
![]() Ответ: а)
Ответ: а) ![]()
0 3 ![]()
Является ли один из
предикатов, заданных на ![]() ¡
¡
3.следствием другого?:
а) ![]() и
и ![]()
Здесь 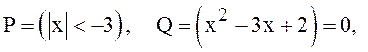
![]()
![]() Значит
Значит ![]()
Ответ: ![]()
![]() и
и ![]()
![]() и
и ![]()
3. Выяснить, равносильны ли следующие предикаты, если дано, что:
1) ![]() ¡ 2)
¡ 2) ![]() 3)
3) ![]() 4)
4)
![]()
![]() и
и ![]()
![]() и
и ![]()
![]() и
и ![]()
4.
Определить значение истинности
полученных из предиката ![]()
![]() навешиванием кванторов высказываний:
навешиванием кванторов высказываний:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответы: ![]()
5. Определить значение истинности следующих высказываний:
![]()
![]()
![]()
Ответы:![]()
Упражнения для самостоятельной работы
1. Найти значение истинности следующих высказываний:
![]()
![]()
![]()
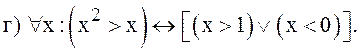
Ответы: ![]()
2. Найти множества истинности следующих предикатов и изобразить их на числовой прямой:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.