Техника кодирования и декодировании цифровых сигналов. Циклические коды (сост. В.И. Васильев, B.C. Давыдов), страница 5

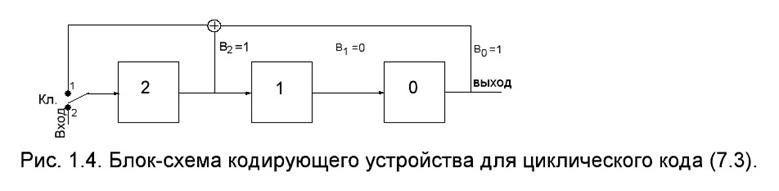
Кодер состоит из регистра памяти РП с сумматором по модулю два. Число ячеек регистра равно числу контрольных символов. Количество связей с сумматором и их место определяется ненулевыми элементами порождающего полинома Р(к).

Ячейки памяти в исходный момент должны содержать нули. Информационные символы подаются на вход кодера, начиная со старшего разряда. Через n тактов на входе кодера получается кодовое слово, а регистр памяти будет содержать нули.

Обозначим выходной сигнал через f_i  содержимое ячейки – через a_ji, входной сигнал через g_i, где I – номер такта, j – номер ячейки. Работу кодера можно описать следующей системой уравнений:

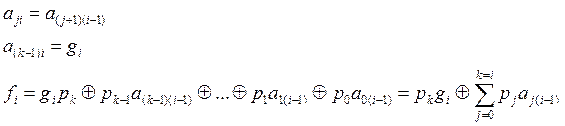(1.27)

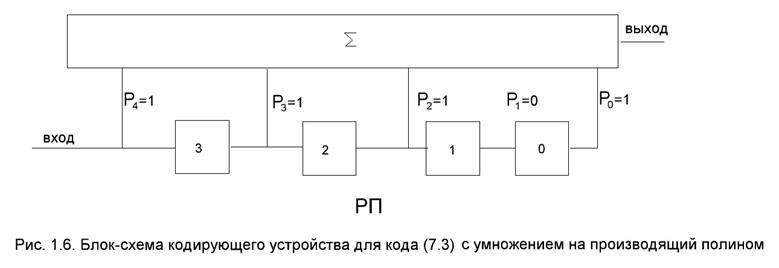
Пример 1.9. Рассмотрим работу кодера для кода (7.3) (рис. 1.6).

Последовательные состояния ячеек регистра сдвига при передаче на вход информационной последовательности сведены в таблицу 1.3.

Таблица 1.3

Номер такта	Информ. символы	Ячейки сдвигающего регистра				Выход
		3	2	1	0
1 2 3 4 5 6 7	0 1 1 -	0 1 1 0 0 0 0	0 0 1 1 0 0 0	0 0 0 1 1 0 0	0 0 0 0 1 1 0	0 1 0 0 1 1 1

, т. Е совпадает с кодовой комбинацией примера 1.8.

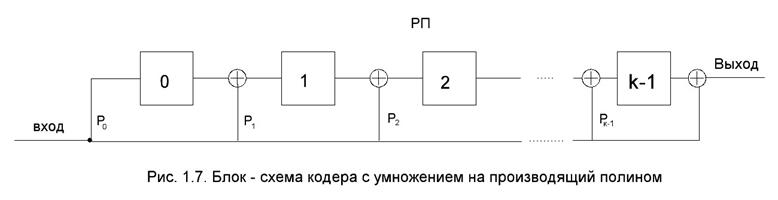
Другая схема умножения G(k) на P(k) приведена на рис. 1.7.

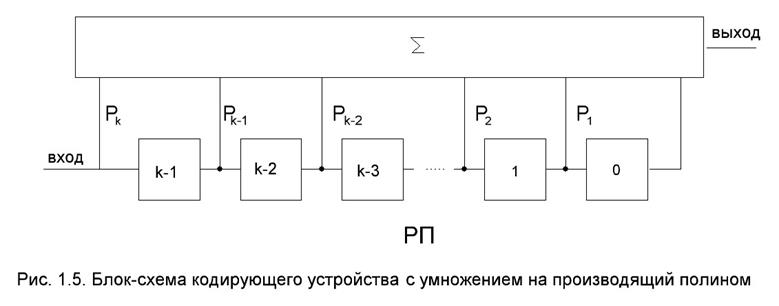
Кодер состоит из к – разрядного регистра сдвига РП и сумматоров по модулю два, число место которых определяется ненулевыми коэффициентами полинома Р(к). Кодовое слово получается за n тактов. Информационные символы подаются начиная со старшего разряда.

Примем обозначения (1.27), работу кодера можно описать следующей системой уравнений:

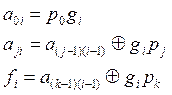           (1.28)

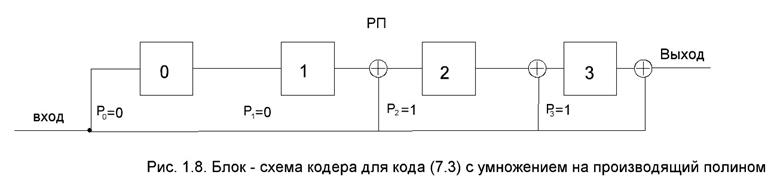
Пример 1.10. Рассмотрим работу кодера для кода (7.3) (рис. 1.8).

Последовательные состояния ячеек регистра сдвига при кодировании информационной последовательности приведены в таблице 1.4.

Таблица 1.4

Номер такта	Информ. символы	Ячейки сдвигающего регистра				Выход
		0	1	2	3
1 2 3 4 5 6 7	0 1 1 -	0 1 1 0 0 0 0	0 1 1 1 0 0 0	0 1 1 1 1 0 0	0 1 0 1 1 1 0	0 1 0 0 1 1 1

, т. Е совпадает с кодовой комбинацией примеров 1.8 и 1.9.

1.5. Методы обнаружения и исправления ошибок в циклических кодах.

Независимо от способа получения кодовая комбинация циклического кода удовлетворяет условиям (1.4) и (1.20).

Эти условия можно переписать в виде:

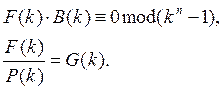        (1.29)

Соотношения (1.29) лежат в основе методов обнаружения и исправления ошибок.  Если при передаче по каналу связи кодовая комбинация   F(K)     искажается,  то соотношения  (1.29) не удовлетворяются.

Пусть под действием помехи х(к) кодовое слово переходит в новое:

.

Когда       (1.30)

Векторы ошибок х(к) можно различать лишь в том случае, если выполняется неравенство

  (1.31)

Полиномы будем называть синдромом ошибки. Если полином принадлежит множеству корректируемых ошибок, то  может быть восстановлен по синдрому   (1.32)

и использован для нахождения F(k) и U(k).

Допустим, что , гдеи выполняется условие (2.31). Найдем синдром ошибки для :

    (1.33)

Отсюда

      (1.34)

т.е. синдром ошибки  приводится к синдрому ошибки . Это обстоятельство позволяет резко упростить декодирующее устройство для циклического  кода.  В комбинации длины n число возможных ошибок кратности   S   и менее определяется формулой  (1.16). Учитывая условие (1.33), для исправления этих ошибок необходимо настроить селектор на синдромы допустимых форм ошибок,  содержащих искажение на первой позиции. Число cелектируемых синдромов определяется по формуле:

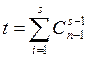            (1.35)

Декодирующее устройство с умножением принятой последовательности на проверочный полином приведено на рис.1.9.