Циклический код будет задан, если указан его порождающий полином P(k). При атом, как и для всякого линейного кода, можно построить порождающую и проверочную матрицы.
Порождающую матрицу можно записать в следующем виде:
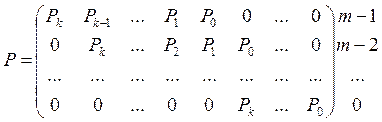 (1.8)
(1.8)
Матрица
Р имеет n столбцов и m=n-k
строк. Ее ненулевые элементы являются коэффициентами производящего полинома ![]()
Проверочная матрица составляется по известному проверочному полиному B(k).
![]()
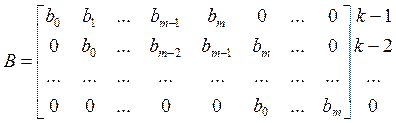
![]() (1.9)
(1.9)
Матрица
В имеет n столбцов и k=n-m
строк, ее ненулевые элементы равны коэффициентам проверочного полинома ![]() .
.
Линейный циклический код полностью определяется порождающим или проверочным полиномом. Зная один из них, можно найти другой и построить производящую и проверочную матрицы.
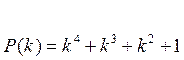
Пример1.2. Для кода примера 1.1 порождающий полином
Производящая матрица в соответствии с (1.8) запишется как
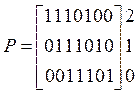
Проверочная матрица в соответствии с B(k) имеет вид:

![]()
Матрицы Р и В можно преобразовать так, чтобы они содержали в себе квадратную единичную матрицу. Такая каноническая форма записи часто применяется при задании систематических кодов. В канонической форме матрица Р запишется в виде:
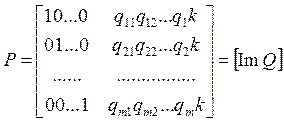 ,
(1.10)
,
(1.10)
Где Im – единичная матрица размерности m×n.
Аналогично для матрицы В:
![]()
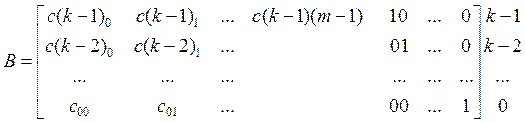 (1.11)
(1.11)
.
Проверочная матрица может быть построена также и из производящей матрицы:
![]()
 (1.12)
(1.12)
Сравнивая выражения (1.11) и (1.12), нетрудно заметить, что матрица С равна транспонированной подматрице Q, т.е.
![]() (1.13)
(1.13)
Отсюда следует, что произведение матриц
![]() (1.14)
(1.14)
По
матрице Р в канонической форме можно определить корректирующую способность
кода. Известно, что для исправления S – кратной ошибки и обнаружения V – кратной ошибки ![]() расстояние Хемминга
расстояние Хемминга ![]() .
При построении систематического кода подматрица Q производящей
матрицы Р должна иметь в строке не менее (d-1) единиц, а
кодовое расстояние между строками должно быть не менее (d-2).
.
При построении систематического кода подматрица Q производящей
матрицы Р должна иметь в строке не менее (d-1) единиц, а
кодовое расстояние между строками должно быть не менее (d-2).
Это положение может быть применено для анализа корректирующей способности циклического кода по матрице вида (1.10).
Пример 1.3 Приведем матрицы Р и В примера 1.2 к канонической форме.
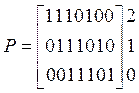
![]()
Пронумеруем
строки снизу вверх и столбцы матрицы слева направо. Так как m=3,
то слева получим единичную матрицу размерности ![]() . Для
этого просуммируем по модулю 2 первую и вторую строки матрицы (получаем 2-ю
строку матрицы в канонической форме), затем первую и нулевую строки матрицы
(получаем 1-ю строку), нулевая строка остается без изменения. Итак, получаем:
. Для
этого просуммируем по модулю 2 первую и вторую строки матрицы (получаем 2-ю
строку матрицы в канонической форме), затем первую и нулевую строки матрицы
(получаем 1-ю строку), нулевая строка остается без изменения. Итак, получаем:
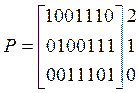
![]()
На основании (1.12) находим проверочную матрицу в канонической форме:
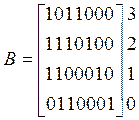
![]()
где третья строка равна третьей строке исходной матрицы, вторая строка равна сумме третьей и второй, первая строка равна сумме первой, второй и третьей, нулевая строка равна сумме всех строк исходной матрицы.
Проверим выполнение условия (1.14):
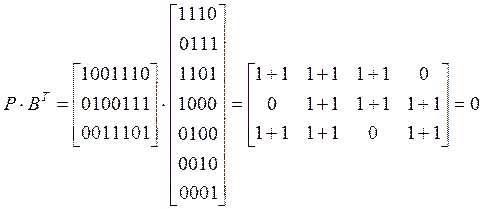
Из матрицы Р в канонической форме можно определить расстояние Хемминга для порождающего циклического кода. Все строки подматрицы содержат по три единицы, а кодовое расстояние между ними равно двум. Следовательно, кодовое расстояние циклического кода d=4.
1.3. Выбор порождающего полинома.
Для
того, чтобы циклический код обладал заданной корректирующей способностью ![]() на порождающий полином Р(k)
накладывается ряд ограничений.
на порождающий полином Р(k)
накладывается ряд ограничений.
Если число всех корректируемых ошибок равно N, а порождающий полином имеет степень k, то должно выполняться условие:
![]() (1.15)
(1.15)
Число корректируемых ошибок определяется из выражения:
 (1.16)
(1.16)
Из
(1.15) и (1.16) находим нижний предел избыточности, необходимой для исправления
ошибок кратности S при ![]() .
.
![]()
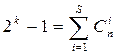 (1.17)
(1.17)
Формула
(1.17) может быть использована для нахождения степени порождающего полинома 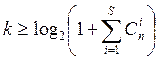 .
.
Расстояние
Хемминга для кода, порождаемого полиномом ![]() ,
всегда не больше чем число отличных от нуля коэффициентов в полиноме P(k).
Это условие позволяет по известному d определить необходимое число не
нулевых элементов в порождающем полиноме.
,
всегда не больше чем число отличных от нуля коэффициентов в полиноме P(k).
Это условие позволяет по известному d определить необходимое число не
нулевых элементов в порождающем полиноме.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.