Книга посвящена технике кодирования и декодировании цифровых сигналов и служит дополнением к пособию "Телемеханика", часть 1. Опыт авторов в чтении соответствующих курсов лекций и руководстве проектами подтвердил необходимость создания специального хорошо иллюстрированного руководства для студентов и инженеров, занимающихся вопросами передачи данных.
Мы старались в достаточно наглядной форме изложить современные методы передачи и приема кодированных сигналов и надеемся, что данная книга поможет широкому кругу специалистов ознакомиться с перспективными методами кодирования и декодирования цифровых сигналов и будет способствовать внедрению этих методов в практической деятельности.
Авторы будут признательны всем лицам, которые пришлют свои замечания, отзывы и пожелания по данному пособию.
Допущено редакционно-издательским советом НЭТИ в качестве учебного пособия
Составил канд. техн. наук В.И. Васильев и аспирант B.C. Давыдов
Ответственный за выпуск ст. преподаватель А.П. Буркни
Кафедра автоматики и телемеханики
Глава 1. ЦИКЛИЧЕСКИЕ КОДЫ
1.1. Определение и основные свойства
Под кодом будем понимать конечное множество целых рациональных чисел, сопоставленных по определенному алгоритму с множеством сообщений. В курсе "Телемеханика” (ч. 1) рассмотрены способы задания кодов и указаны конструктивные методы построения кодирующих и декодирующих устройств. Остановимся более подробно на критериях приемлемости и технике кодирования и декодирования цифровых последовательностей.
При
дальнейшем рассмотрении основное внимание будет уделено вопросах техники
кодирования и декодирования равновероятных сообщений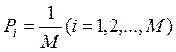 ,
представляемых последовательностью символов
,
представляемых последовательностью символов![]() .
Элементы множества
.
Элементы множества ![]() носят название кодовых комбинаций.
Число n определяет
значность (длину) кодового слова. Канал передачи информации описывается
стохастической матрицей
носят название кодовых комбинаций.
Число n определяет
значность (длину) кодового слова. Канал передачи информации описывается
стохастической матрицей
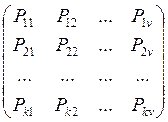
в
которой ![]() . Для симметричного двоичного канала
матрица имеет вид
. Для симметричного двоичного канала
матрица имеет вид
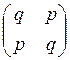 , где
, где ![]() ; р - вероятность искажения передаваемого
символа.
; р - вероятность искажения передаваемого
символа.
Обнаружение r и исправление S ошибок в таком канале достигается, если кодовое расстояние d удовлетворяет условию d = r +S + 1 . Код является оптимальным в смысле кодового расстояния в том случае, если среди всех кодов с теми же значениями n и М нет больше кодов с большим расстоянием Хемминга.
Если ошибки взаимонезависимы,
то вероятность появ![]() ления
ошибки декодирования удовлетворяет неравенству
ления
ошибки декодирования удовлетворяет неравенству
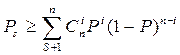
При p<<1 можно воспользоваться приближенным неравенством
![]()
Групповые коды, обеспечивающие максимальную вероятность правильного декодирования при заданных n и k, являются оптимальными по Слепяну.
Целесообразность применения корректирующих кодов следует из условия
![]()
![]()
т.е. когда корректирующий код обеспечивает, по крайней мере, меньшую вероятность ошибки по сравнению с равнодоступным кодом. При равноскоростном сравнении выигрыш в помехоустойчивости в случае применения корректирующего кода получается, если удовлетворяется критерий Финка
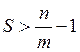 .
.
Групповые коды, удовлетворяющие критерию Финка , называются оптимальными. Заметим, что оптимальные групповые коды, для которых соблюдается условие
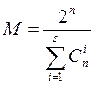
относятся к совершенным (сомкнуто-упакованным кодам). Квази-совершенные коды отличаются от совершенных тем, что помимо исправления всех ошибок кратности S могут исправлять некоторые ошибки кратности S+1.
Важнейшие случаем групповых кодов являются групповые циклические коды.
Циклический
линейный код определяется как множество n - значных
комбинаций, которые наряду со свойствами обычных систематических кодов обладают
еще одним: если комбинация /![]() / принадлежит
циклическому коду, то комбинация /
/ принадлежит
циклическому коду, то комбинация /![]() /, полученная из нее
циклическим сдвигом, также принадлежит этому коду.
/, полученная из нее
циклическим сдвигом, также принадлежит этому коду.
Пример 1.1. Множество комбинаций
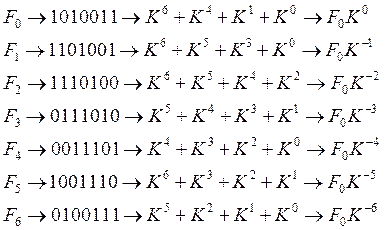
![]()
образует
семизначный циклический код с кодовым расстоянием ![]() . Справа
дана алгебраическая форма записи комбинации в виде полинома
. Справа
дана алгебраическая форма записи комбинации в виде полинома
![]() .
.
![]()
Циклический
сдвиг вправо на ![]() шагов, равносилен умножению
исходной кодовой комбинации, на
шагов, равносилен умножению
исходной кодовой комбинации, на![]() . При атом операция
умножения выполняется по модули многочлена
. При атом операция
умножения выполняется по модули многочлена ![]() (многочлены
перемножаемся и результат делится на
(многочлены
перемножаемся и результат делится на![]() по обычным правилам;
получившийся при этом остаток представляет собой искомое произведение). Так
как
по обычным правилам;
получившийся при этом остаток представляет собой искомое произведение). Так
как ![]() , то
, то
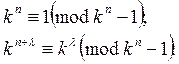
![]()
Пример 1.1а. Нейдем
комбинацию ![]() , используя известную
из примера 1.1 комбинацию
, используя известную
из примера 1.1 комбинацию ![]() .
.
![]() Для всех комбинаций
Для всех комбинаций ![]() циклического кода выполняется условие
циклического кода выполняется условие
![]()
![]()
где
![]()
![]()
Есть некоторый полином
степени k>n , причем двучлен 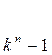 должен делиться на
должен делиться на ![]() без остатка:
без остатка: ![]()
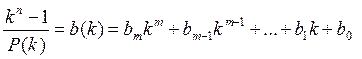
![]()
Из выражения (1.6)
следует: 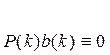
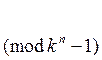 . (1.7)
. (1.7)
Для примера 1.1 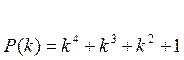 ,
,
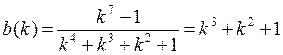
Полипом P(k) называют порождающим, его степень k определяет число контрольных символов в кодовой комбинации. Полином b(k) называет проверочным, его степень mопределяет число информационных символов.
1.2. Способы задания циклических кодов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.