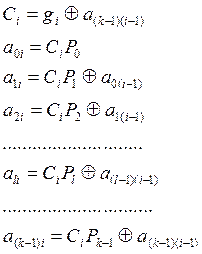Техника кодирования и декодировании цифровых сигналов. Циклические коды (сост. В.И. Васильев, B.C. Давыдов), страница 4

         (1.22)

Пример1.6  Блок – схема кодирующего устройства для кода (7.3) с представлена на рис.1.2.

Для кодирования возьмем информационную последовательность примера 1.5 . Последовательные состояния ячеек регистра сдвига приведены в таблице 1.1.

Таблица 1.1.

Второй способ формирования комбинации циклического кода основан на свойстве проверочного полинома B(k). Блок – схема такого кодирующего устройства приведена на рис. 1.3.

Кодер состоит из регистра памяти РП с сумматором по подулю два в цепи обратной связи. Число ячеек регистра определяется степенью m проверочного полинома. Количество связей с сумматором по модулю два и их место определяются ненулевыми элементами полинома В(К) (коэффициентами b_i ).

В исходном состоянии обратная связь разомкнута,  ключ установлен в положение 1. В регистр РП вводится информационная последовательность G(k) , начиная со старшего разряда. Через m тактов (т.е. после ввода информационных символов) ключ переводится в положение 2. На выход выдается информационная последовательность, а в регистре РП формируются контрольные символы. Формирование контрольной последовательности заканчивается черев k тактов  (m+k   тактов о начала работы). После этого ключ переводится в положение 1 и контрольная последовательность выдается на выход . кодирующего устройства в течение m тактов. На вход кодера при этом подается нулевая последовательность или новая информация. Ввод информации в регистр может осуществляться также и параллельным способом.

Работу кодера можно описать следующими уравнениями (обратная связь замкнута):

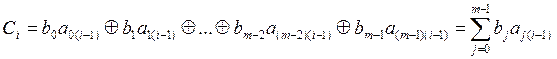    (1.23)

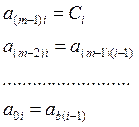
Обозначения приняты аналогично (1.22). Суммирование, как и раньше, ведется по модулю два.

Пример 1.7.  На рисунке 1.4 представлена блок – схема кодирующего устройства для кода (7.3) с проверочным полиномом .

Для кодирования возьмем информационную последовательность

Последовательные состояния ячеек регистра сдвига представлены в таблице 1.2.

Таблица 1.2

Выходная последовательность                                         совпадает с кодовой комбинацией 1.5 и 1.6.

Третий способ формирования комбинаций циклического кода состоит в следующем. Один из базисов циклического кода совпадает с комбинациями, соответствующими полиномам , где , то есть порождающую матрицу можно записать в виде: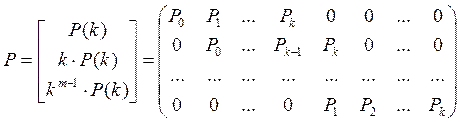

Любая комбинация F_j циклического кода может быть представлена через базисные комбинации матрицы Р в виде: 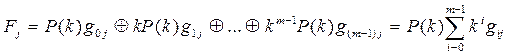.    (1.25)

Под знаком суммы стоит информационная последовательность ,

Отсюда кодовая комбинация .       (1.26)

Для получения комбинации циклического кода информационную последовательность нужно умножить на производящий полином.

Пример 1.8. Найдем кодовую комбинацию для кода (7.3) с .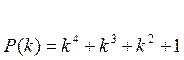

Пусть дана . Тогда .Укажем, что закодированная последовательность не содержит информационные символы в явном виде, но удовлетворяет условиям (1.4)+(1.20).

Итак, для получения кодовой комбинации необходимо иметь устройство для умножения многочленов. Блок-схема такого устройства приведена на рис.1.5.