Техника кодирования и декодировании цифровых сигналов. Циклические коды (сост. В.И. Васильев, B.C. Давыдов), страница 3

После выбора полинома  P(k) необходима дополнительная проверка, например, по условию (1.10), т.к. накладываемые ограничения являются необходимыми, но не достаточными.

Если код предназначается для исправления пакетов ошибок длины l и менее, то порождающему полиному предписывается следующее требование: при любом разделении полинома P(k) на две части, хотя бы в одной должны находится ненулевые элементы, показатели степеней которых отличаются не менее, чем на l.

Число ошибок длины l и менее равно

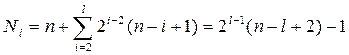            (1.18)

Учитывая (1.15), находим:                                                     (1.19)

По этим необходимым, но недостаточным условиям можно ориентировочно оценить корректирующую способность кода, порождаемого полинома P(k).

Пример 1.4. Определить корректирующую способность кода (7.3), порождаемого полиномом .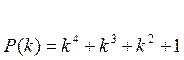

Число ненулевых элементов в порождающем полиноме равно четырем, значит, кодовое расстояние . Число ошибок в кодовой комбинации:

- одиночных -

- двоичных -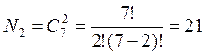

Используя (1.17), имеем:

  , т.е. код позволяет исправлять лишь одиночные ошибки. В примере 1.3 приведен анализ корректирующей способности данного кода с использованием порождающей матрицы Р в форме (1.10).

Для определения длинны пакетов ошибок, исправляемых данным кодом, разобьем полином P(k) на две части и каждый раз посчитаем максимальную разность показателей степеней в одной из частей. Минимальная разность из получаемых и будет ответом.

сечение 1: 4-2=2, сечение 2: 2-0=2, сечение 3: 3-0=3.

Минимальная разность равна двум, а отсюда .

Из (1.19) получаем:

.

Итак, данный код является квазисовершенным и обеспечивает исправление всех одиночных и двойных смежных ошибок.

1.4. Методы формирования циклических кодов.

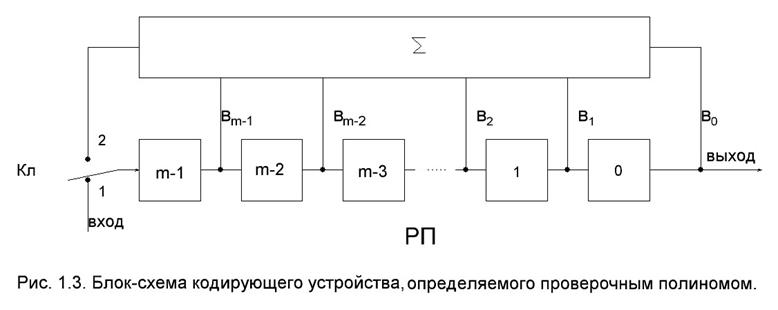
В процессе кодирования нужно найти значения контрольных символов, при которых произведение вектора кодовой комбинации на проверочную матрицу В равняется нулю.

                                                         (1.20)

Это равенство выполняется, если вектор кодовой комбинации делиться без остатка на производящий полином P(k), т.е. должно выполняться условие (1.4). Отсюда определяется метод нахождения кодовой комбинации: необходимо информационную последовательность

умножить на , разделить на производящий полином P(k) и остаток R(k) прибавить к G(k).

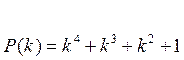
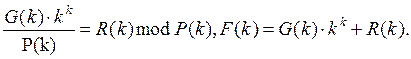   (1.21)

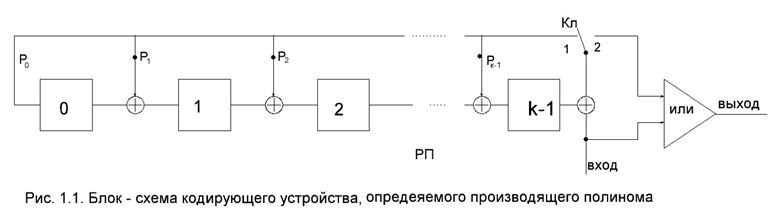
Пример 1.5 Найдем кодовую комбинацию для кода (7.3) порождаемого полиномом

. Пусть дана информационная последовательность  Тогда

Выполним деление на P(k): остаток

Кодовая комбинация совпадает с комбинацией F_s примера 1.1 и имеет вид:

Для реализации данного метода необходимо иметь устройство,  вычислявшее остаток от деления многочлена  на производящий полином Р(К) .  Блок-схема кодирующего устройства с деленном на производящий полином представлена на рис.  1.1.

Кодирующее устройство состоит ив регистра памяти РП,  число ячеек которого равно степени порождающего полинома, с обратными связями. Количество сумматоров по модулю 2 определяется числом ненулевых элементов без одного в   Р( К)   ,  а их место - коэффициентами P_i.

В исходном состоянии ключ  Кл  установлен в положение 1. На вход последовательно подаются символы ,  начиная со старшего разряда,  одновременно эти символы поступают через схему ИЛИ на выход кодера. Через m=n-k тактов в регистре памяти РП    вырабатывается остаток R(K) от деления на Р(К)  , ключ переводится  в положение 2 и на выход кодера выдаются контрольные символы (k тактов). Через n тактов на выходе имеем кодовую комбинацию.

Правило заполнения ячеек регистра  памяти РП: в ячейку, на выходе которой стоит сумматор по модулю два, результат записывается равным сумме по модулю два содержимого  предшествующей ячейки (предыдущий тракт) и сигнала обратной связи на денной такте; сигнал обратной связи равен сумме по модулю два содержимого последней ячейки (предыдущий такт) и информационного символа на данном такте. Если обозначать сигнал обратной связи через С_i, входной информационный сигнал через g_i, а содержимое ячейки через a_ji, где i – номер такта,  j – номер ячейки, то работу кодера с замкнутой обратной связью можно описать следующей системой уравнений: