Допуски и посадки. Шероховатость поверхностей

5. ДОПУСКИ И ПОСАДКИ

5.1. Основные понятия и определения

При сборке сопрягаемых деталей, входящих одна в другую, различают охватывающую поверхность (отверстие) и охватываемую (вал). Размер сопрягаемых поверхностей отверстия и вала носит общее название номинального размера соединения, который одинаков для отверстия и для вала. Его округляют до стандартного значения по ГОСТ 6636 (Прил. Г) и проставляют на чертежах.

Обеспечить точно номинальный размер невозможно никакими технологическими приёмами. В подавляющем большинстве случаев в этом и нет необходимости. Действительный размер, получаемый обработкой и измеряемый специальным инструментом, должен находиться между предельными, ограниченными стандартом, размерами.

Разность между размерами отверстия и вала определяет посадку, т.е. характер соединения сопряжённых деталей,которая может быть с зазором, с натягом и переходной, допускающей как зазор, так и натяг.

Принята международная буквенно-цифровая система обозначений предельных отклонений размеров от номинала (ГОСТ 25347). Отклонения а – h (для валов) и А – Н (для отверстий) предназначены для образования полей допусков и посадок с зазором; р – zс (Р – ZC) – для обеспечения гарантированного натяга (прессового соединения); j_s, k, m, n (J_s, К, М, N) дают переходные посадки.

На рис. 28 представлено соединение с зазором, где D = d – номинальный размер. Наибольший и наименьший предельные размеры определяют по зависимости: для отверстия

                                               (31)

для вала

                                             (32)

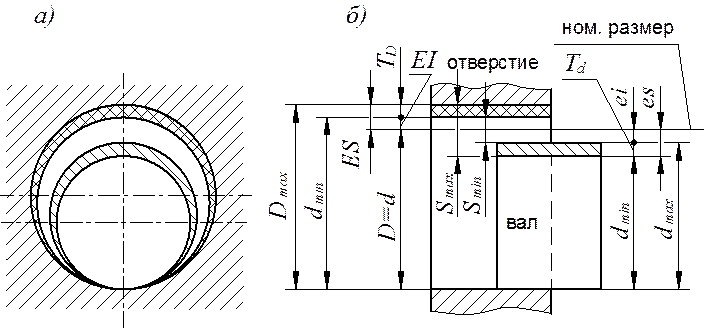Рис. 28. Соединение с зазором

В формулах (31) и (32) D_max и D_min – предельные размеры отверстия, d_max и d_min– предельные размеры вала,  EI и ei – основные отклонения соответственно отверстия и вала, минимальные по абсолютной величине; ES – максимальное предельное отклонение отверстия; es – максимальное предельное отклонение вала. Предельные отклонения:

                                       (33)

где IT_D – допуск отверстия, определяемый как разность между предельными отклонениями; IT_d – допуск вала.

Величины ES и es зависят от квалитета (quality – качество, имеет смысл класса точности), по которому назначается допуск IТ (I – ИСО, Т – Toleranz – допуск). Установлено 20 квалитетов, из которых квалитеты 6...8 характеризуют высокую точность размеров, а квалитеты 12... 15 используют для свободных размеров. Если назначить для вала 6-й квалитет, а для отверстия 7-й, то в формуле (33) можно записать IT6вместо IT_d и IT7 вместо IT_D.

Разнообразные посадки получают путём изменения предельных отклонений одной детали, оставляя неизменными предельные отклонения другой детали, являющейся основной деталью системы. В системе отверстия, являющейся предпочтительной по техническим и экономическим соображениям, минимальное предельное отклонение EI = 0.

Каждый из заштрихованных прямоугольников на рис. 28, ограниченных верхним и нижним отклонениями, называется полем допуска. На рисунке показаны поля допусков с зазорами от S_min = D_min – d_max до S_max = D_max – d_min. Предельные отклонения наиболее распространенных размеров и посадок приведены в табл. 10.

5.2. Расчёт посадок с гарантированным натягом

Прессовую посадку ступицы одного из колёс редуктора на вал студент должен рассчитать, а в других аналогичных соединениях принять такими же. Расчётная схема соединения представлена на рис. 29. На схеме показаны: d – номинальный размер соединения; d₁ и d₂ – диаметры вала (внутренний) и втулки (наружный); l – длина ступицы;F_a – осевая сила; Т – крутящий момент.

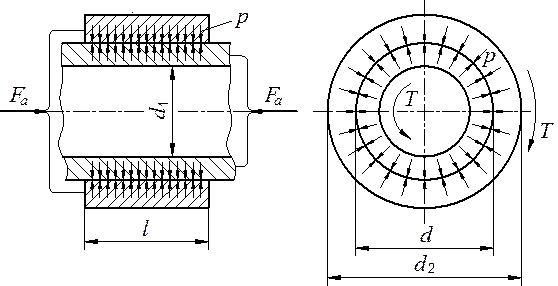Рис. 29. Расчётная схема соединения с натягом

По теории расчёта толстостенных сосудов давление на поверхности контакта в МПа в зависимости от натяга определяют по формуле Лямэ:

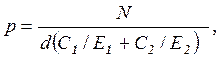                                           (34)

где  N – расчётный натяг, мм; С₁ и С₂ – коэффициенты задачи Лямэ; Е₁ и Е₂ – модули упругости, МПа.

Коэффициенты С₁ и С₂ определяют по формулам:

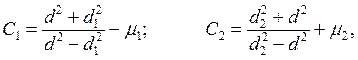                             (35)

где μ₁ и μ₂ – коэффициенты Пуассона.

          Таблица 9

      Таблица 10. Предельные отклонения, мкм