Допуски и посадки. Шероховатость поверхностей, страница 3

Примечания.     1. Звёздочками показаны предпочтительные поля допусков.

2.Поля допусков отверстия и вала симметричны.

3.Другие поля допусков приведены в справочниках [1, 2, 8].

Расчётный натяг

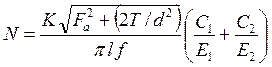,                                        (36)

где K – коэффициент запаса сцепления; принимать K = 1,5… 2; в ответственных соединениях до K = 3; F_a – осевая сила, Н; Т – крутящий момент, Н·мм; f – коэффициент трения; принимать в зависимости от материалов соединения по табл. 11, где приведены и другие характеристики материалов.

Таблица 11. Характеристики материалов прессовых соединений

Параметры	Материал втулки
	Сталь	Чугун	Бронза
Модуль упругости  Е, МПа	21,5·104	14·104	1,1·104
Коэффициент Пуассона  m	0,3	0,25	0,33
Коэффициент трения  f  при сборке: механической	0,06…0,13	0,07…0,12	0,05…0,1
тепловой	0,14…0,16	0,07…0,09	0,05…0,14

Примечания.  1. Охватываемая деталь из стали или чугуна. 2. При отсутствии смазки принимать верхнее значение коэффициентов трения  f.

Поправка на шабровку (вводится только для механической сборки)

                                        (37)

где R_z1 и R_z2 – максимальные высоты шероховатостей посадочных поверхностей, мм; рекомендуются для прессовых соединений следующие сочетания шероховатостей: R_z1/R_z2 = 0,0063/0,01; 0,0032/0,0063 мм.

Технологический натяг

                                                    (38)

По технологическому натягу на первом этапе проектного расчёта выбирают посадку ( см. табл. 10) с выполнением условия

                                                   (39)

где - минимальный табличный натяг.

     На втором этапе проектного расчёта принимают более лёгкую посадку и проверяют её пригодность при вероятности Р < 1 (0,999...0,95). Условие пригодности второй посадки

,                                                     (40)

где N_Pmin – минимальный вероятностный натяг.

Предельные табличные натяги N_min и N_max не отражают степени надёжности соединений. Распределение действительных размеров по полям допусков делает маловероятной сборку соединений из деталей с предельными размерами. Поэтому, обрезая «хвосты» кривых распределения действительных размеров и допуская тем самым вероятность разрушения соединений, можно увеличить минимальный и снизить максимальный табличные натяги (рис. 30). Полученные таким образом натяги называют вероятностными.

        

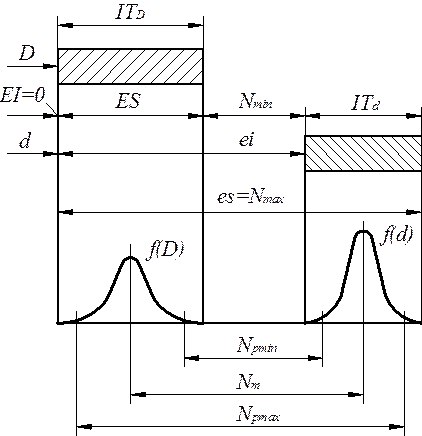
Рис. 30. Поля допусков и кривые нормального распределения

Площадь под кривой распределения считают равной 1. После обрезания «хвостов» она уменьшается. Например, при вероятности неразрушения Р = 0,99 она составляет 0,99. При нормальном законе распределения размеров вероятностные натяги определяют по формулам:

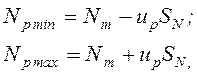                                     (41)

где  N_m – средний натяг; u_p – квантиль нормального распределения; S_N – среднее квадратичное отклонение табличного натяга.

Средний натяг определяют средними значениями отклонений:

.                             (42)

Среднее квадратичное отклонение табличного натяга

                                                 (43)

.                                 (44)

Квантиль нормального распределения принимает следующие значения в зависимости от вероятности Р неразрушения (неразбираемости) соединения (табл. 12).

Таблица 12. Квантили нормального распределения

Р	0,9	0,95	0,99	0,995	0,999
up	1,28	1,64	2,33	2,58	2,9

Вероятностные натяги, рассчитанные для различных посадок по формулам (41)…(44), приведены в табл. 13, которой можно пользоваться при назначении табличных и вероятностных натягов.

На основании неравенств (39) и (40) делают окончательный выбор посадки. Для гладких валов необходимо сделать пересчет из системы отверстия в систему вала (см. пример 10).

Пример 8. Рассчитать посадку ступицы на цилиндрический вал с номинальным диаметром d = 50 мм, внутренним диаметром вала d₁ = 0, наружным диаметром ступицы d₂= 70 мм и длиной ступицы  l = 80 мм. Материал деталей – сталь (Е = 21,5·10⁴ МПа, m = 0,3). Крутящий момент Т = 240 Н×м; осевая нагрузка F_a = 800 Н. Сборка тепловая.