Теоретические основы электротехники. Электрические цепи синусоидального тока (установившиеся процессы): Учебное пособие, страница 8

Решение. Условие полной компенсации потери напряжения в линии может быть записано в виде ;  или

Откуда

 ,

 где

По данным предыдущей задачи определяем R₂; Х₂; (выбираем режим работы линии, соответствующей току ).

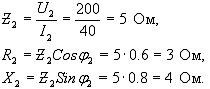
Имеем ,

откуда .

Подставляя численные значения величин, получим

,

 Ом,

 Ом.

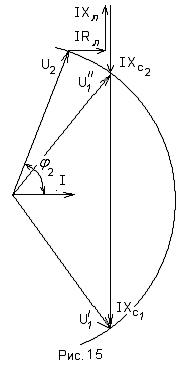
Векторная диаграмма компенсированной линии построена на рис.15.

            12. Определить токи и напряжения всех участков цепи (рис.16).

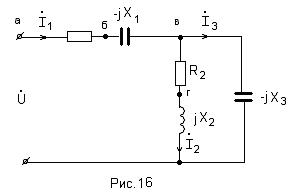
Построить топографическую диаграмму напряжений, совместив ее с векторной диаграммой токов.

 В,  Ом,  Ом,  Ом, .

Решение. Для определения недостающих сопротивлений используем условие .

,

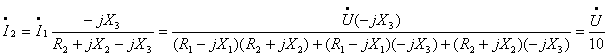отсюда .

Подставляя численные значения и приравнивая вещественные и мнимые части, получим два уравнения:

;

.

Решая систему уравнений, находим Х₃=8 Ом, Х₁=10 Ом.

Зная параметры цепи, легко найти токи и напряжения всех участков.

Ответ.  А;  А;  А.

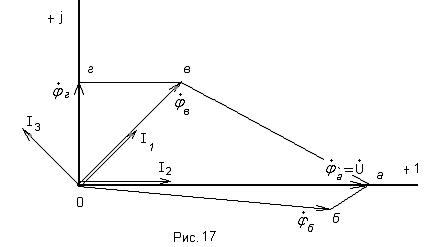
Топографическая диаграмма построена на рис.17.

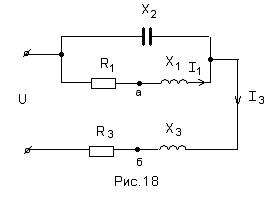
            13. Определить сопротивление Х₃ цепи (рис.18), если сумма действующих значений напряжений и  равна действующему значению входного напряжения  и  Ом.

Решение. Выразим комплексы напряжений  и  через комплекс напряжения :

;

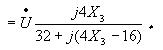
Модули этих напряжений будут равны