Теоретические основы электротехники. Электрические цепи синусоидального тока (установившиеся процессы): Учебное пособие, страница 11

Исключая ток  и подставляя численные значения величин, получим , .

Откуда  и  А.

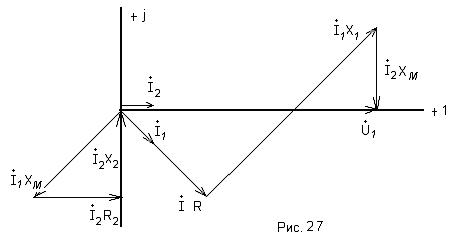
Векторная диаграмма цепи, построенная по уравнениям  и  показана ни рис.27.

Для первого контура уравнения баланса мощностей получим, умножив уравнение  на сопряженный комплекс тока ,

или

.

Для второго контура

или

.

В полученных уравнениях - соответственно активная и реактивная мощность источника,  и - соответственно активные и реактивные мощности первого и второго() контуров,  и - активные мощности взаимоиндукции,  и - реактивные мощности взаимоиндукции.

Подставляя численные значения величин, найдем

 Вт,  Вт,

 вар,  вар,

 Вт,  Вт,  вар,

 вар,  Вт,  вар.

Следует обратить внимание на то, что в данном случае первая катушка передает энергию второй ( P_M1>0 , а Р_М2 <О   ). Складывая уравнения балансов мощностей контуров и учитывая, что, а , получим уравнения баланса мощностей всей цепи.

или

1728 = 1152 + 576 (Вт),

1728 = 2304 + 576 – 2*576 (вар).

23. В цепи (рис.26) исключить индуктивную связь.

Решение. Преобразуем уравнения цепи

,

,

прибавим к обеим частям первого , а к обеим частям второго . Тогда

,

.

Этим уравнениям соответствует электрическая цепь без индуктив­ной связи (рис.28).

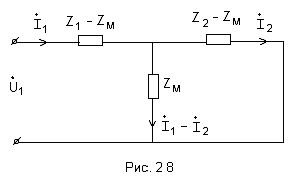
Замечание. При расчете цепей с индуктивной связью часто используются преобразования схем, показанные на рис.29.