Расчет неразрезных балок, страница 9

i

10.3.2.Определение моментных фокусных отношений

Формулы  (10.34),  (10.35),  поясняющие  суть  моментных  фокусных отношений, не позволяют находить численные значения этих отношений. Входящие в эти формулы опорные моменты являются неизвестными вели- чинами.

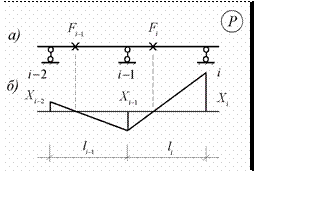Для получения формулы, позволяющей определять величины левых моментных фокусных отношений, рассмотрим два произвольных незагру- женных  пролета  неразрезной  балки,  по  отношению  к  которым  нагрузка располагается справа (рис.10.24.а)

Рис.10.24

В этом случае  эпюра моментов в этих пролетах пройдет через  левые мо- ментные  фокусы.  Возможное  очертание  эпюры  моментов  показано  на рис.10.24.б. Тогда опорные моменты, обозначенные на эпюре, будут связаны друг с другом следующими соотношениями

X i -1

= - X i  , ki

X i -2

= - X i -1   =

ki -1

X i

ki -1ki

(10.36)

Запишем уравнение трех моментов для i-1–ой промежуточной опоры

~

li -1 X

i -2

~

+ 2(

li

li -1

+ ~)X

+

i -1

~

li X i   = 0

(10.37)

Подставим соотношения (10.36) в (10.37) и после несложных преобразований уравнение примет вид

~

li -1

~

- 2(

li

li -1

+ ~)k

+

i -1

~

li k

i -1ki   = 0

Разрешая уравнение относительно

~

ki , получим формулу

l    ⎛     1  ⎞

k  = 2 +   i~-1 ⎜ 2 -       ⎟

i                      l          k

(10.38)

i    ⎝        i -1  ⎠

Формула (10.38) позволяет вычислять левое моментное фокусное отноше- ние  произвольного  пролета  через  левое  моментное  фокусное  отношение предшествующего  ему  пролета.  Она  позволяет  осуществлять  цепочечные вычисления левых моментных фокусных отношений и поэтому называется рекуррентной формулой для их вычисления.

Для получения аналогичной формулы, позволяющей определять ве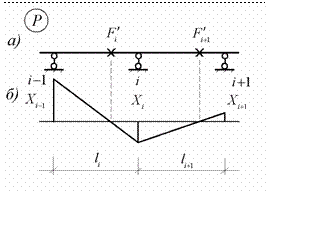личины правых моментных фокусных отношений, рассмотрим два произ- вольных  незагруженных  пролета  неразрезной  балки,  по отношению  к  ко- торым нагрузка располагается слева (рис.10.25.а)

Рис.10.25

В этом случае эпюра моментов в этих пролетах пройдет через правые моментные  фокусы.  Возможное  очертание  эпюры  моментов  показано  на

рис.10.24.б. Тогда опорные моменты, обозначенные на эпюре, будут связаны друг с другом следующими соотношениями

X  = - X i -1  ,

i                  k¢

X i +1

= - X i

k¢

=  X i -1

k¢k¢

(10.39)

i                                          i +1

i    i +1

~

Запишем уравнение трех моментов для i–ой промежуточной опоры

~

li X

li

i -1

+ 2(~

li +1 )X i

~

+

+

li +1 X

i +1  = 0

(10.40)

Подставим соотношения (10.39) в (10.40) и после несложных преобразова

+

ний уравнение примет вид

~

l k¢k¢

- 2(~    ~

)k¢      ~   = 0

i    i    i +1

i          i +1

i +1

i +1

+

l

Разрешая уравнение относительно

l

l

~

ki¢ , получим формулу

l    ⎛     1  ⎞

i

k¢ = 2 +   i~+1 ⎜ 2 -       ⎟

(10.41)

¢

li    ⎝

ki +1  ⎠