Расчет неразрезных балок, страница 8

X 3   = -2 l2  ~ l3   - l2

(10.32)

X 2                          l3

l3   k2

Из (10.32) следует, что и в третьем незагруженном пролете опорные моменты имеют разные знаки, их отношение не зависит от нагрузки, а мо- дуль этого отношения не менее 2.

Обобщая соотношения (10.30), (10.32), получим, что в произвольном

i-том незагруженном пролете соотношение опорных моментов имеет вид

~  + ~                 1

X i

X i -1

= -2 li -1 ~  li

li

- li -1

li

(10.33)

Тогда,  в  соответствии  с  соотношениями  (10.30),  (10.32),  (10.33),  следует, что в незагруженных пролетах неразрезной балки (рис.10.21) опорные мо- менты обладают следующими свойствами.

Первое   свойство.   Опорные   моменты   по   концам   незагруженных пролетов имеют разные знаки.

Второе  свойство.  Отношение  опорных  моментов  по  концам  незагруженных пролетов не зависит от нагрузки, а зависит только от жесткостных и геометрических параметров неразрезной балки.

Третье  свойство.  На  эпюре  моментов  в  незагруженных  пролетах имеется инвариантная нулевая точка, положение которой не зависит от нагрузки, а полностью зависит только от жесткостных и геометрических параметров неразрезной балки.

Четвертое  свойство. Опорные моменты  в незагруженных  пролетах убывают по модулю по мере удаления от загруженного пролета неразрез- ной балки.

Инвариантная  нулевая  точка  на  эпюре  моментов  незагруженного пролета называется моментным фокусом. Поэтому установленные четыре свойства  и  называются  фокальными  свойствами  неразрезной  балки.

Они описывают закономерности в распределении изгибающих моментов в незагруженных  пролетах  неразрезной  балки.  Эти  свойства  справедливы при условии расположения нагрузки с одной стороны по отношению к незагруженным  пролетам.  Частным  случаем  такого  расположения  нагрузки является загружение одного пролета.

В зависимости от расположения нагрузки по отношению к незагруженному пролету различают два вида моментных фокуса – левый и правый моментные фокусы.

Левым   моментным   фокусом   называется   инвариантная   нулевая точка  на  эпюре  моментов  незагруженного  пролета  при  условии,  что  на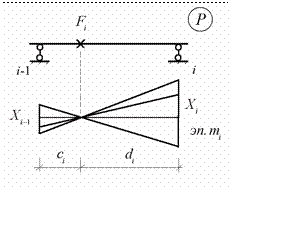грузка располагается справа от этого пролета (рис.10.22)

Рис.10.22

На рис.10.22 левый моментный фокус i – того пролета обозначен Fi.

Правым  моментным  фокусом  называется  инвариантная  нулевая точка  на  эпюре  моментов  в  незагруженном  пролете  при  условии,  что  на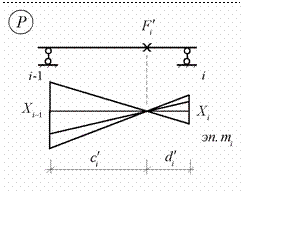грузка располагается слева от этого пролета (Рис.10.23)

Рис.10.23

На рис.10.23 правый моментный фокус i – того пролета обозначен F'i.

С понятием моментного фокуса связано понятие моментного фокусного  отношения.  Моментным  фокусным  отношением  называется  абсолютная величина отношения большего опорного момента незагруженного пролета к меньшему опорному моменту этого пролета. Различают два вида моментных фокусных отношений – левое и правое. Будем обозначать ле- вое  моментное  фокусное  отношение  k  и  правое  моментное  фокусное  от- ношение k'  .

В соответствии с рис.10.22 левое моментное фокусное отношение

i – того пролета описывается следующим отношением опорных моментов

k  = -  X i

(10.34)

i

а  в  соответствии  с  рис.10.23  правое  моментное  фокусное  отношение

i – того пролета описывается следующим отношением опорных моментов

k'   = - X i -1

i                  X

(10.35)