 Построим объемлющую эпюру изгибающих моментов для
трехпро- летной неразрезной балки.
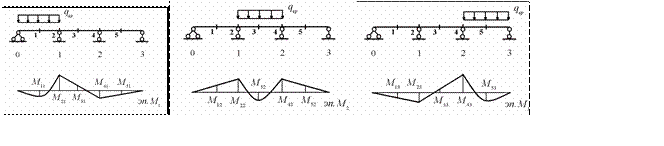
Загрузим поочередно каждый пролет временной нагрузкой и, используя моментные фокусные отношения, построим
эпюры моментов (рис.10.31)
Построим объемлющую эпюру изгибающих моментов для
трехпро- летной неразрезной балки.
Загрузим поочередно каждый пролет временной нагрузкой и, используя моментные фокусные отношения, построим
эпюры моментов (рис.10.31)
Рис.10.31
Ординаты на эпюрах моментов имеют два индекса. Первый индекс указы- вает номер расчетного сечения, в котором определяется изгибающий мо- мент, а второй индекс указывает номер загруженного пролета.
Тогда максимальные изгибающие моменты в каждом расчетном сечении получаются сложением соответствующих положительных величин моментов. Например, для перового расчетного сечения получим
M1max = M11 + M13
и, следовательно, опасным положением временной нагрузки для этого се- чения является ее одновременное расположение в первом и третьем проле- тах.
Минимальные значения изгибающих моментов в каждом расчетном сечении получают сложением соответствующих отрицательных величин моментов. Например, для второго расчетного сечения получим
M 2 min = M 21 + M 22
и, следовательно, опасным положением временной нагрузки для этого сечения является одновременное нагружение первого и третьего пролетов.
Откладывая в каждом расчетном сечении, найденные для него максимальные и
минимальные значения изгибающих моментов и соединяя, соответственно, вершины положительных и отрицательных ординат, полу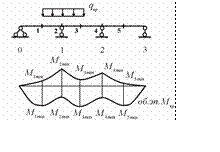 чим объемлющую эпюру изгибающих моментов (рис.10.32)
чим объемлющую эпюру изгибающих моментов (рис.10.32)
Рис.10.32
10.5. Резюме
Неразрезная балка является внешне статически неопределимой кон- струкцией, используемой для перекрытия пролетов в сооружениях различ- ного назначения.
Расчет неразрезной балки обычно производится методом сил с использованием основной системы в виде многопролетной шарнирной балки, получаемой введением шарниров во все промежуточные опорные сечения неразрезной балки.
Канонические уравнения метода сил для такого варианта основной системы неразрезной балки называются уравнениями трех моментов и они имеют вид трехдиагональной ленточной системы линейных неоднородных алгебраических уравнений.
Распределение изгибающих моментов в незагруженных пролетах не- разрезной балки, при условии расположения нагрузки по отношению к ним с одной стороны, подчиняется определенным закономерностям. Эти закономерности описываются фокальными свойствами неразрезной балки.
Использование фокальных свойств позволяет находить изгибающие моменты в неразрезной балке без составления и решения уравнений трех моментов. Такой метод нахождения изгибающих моментов называется ме- тодом моментных фокусных отношений.
Расчет неразрезных балок на действие временной нагрузки связан с построением объемлющих эпюр внутренних усилий. Существует два спо- соба построения таких эпюр – точный и упрощенный.
10.6. Материалы для самоконтроля
Проверьте, как Вы усвоили следующие понятия, определения, алгоритмы и формулы:
- неразрезная балка;
- типы неразрезных балок;
- нумерация опор и пролётов;
- степень статической неопределимости;
- основные системы метода сил для неразрезных балок;
- канонические уравнения метода сил;
- уравнения трёх моментов для нагрузки;
- уравнения трёх моментов для осадки опор;
- решение системы уравнений трёх моментов;
- формулы для определения окончательных изгибающих моментов и поперечных сил от нагрузки;
- формулы для определения окончательных изгибающих моментов и поперечных сил от осадки опор;
- формулу для определения опорной реакции на произвольной опоре неразрезной балки;
- фокальные свойства;
- моментные фокусы;
- формулы для вычисления моментных фокусных отношений;
- интервал изменения моментных фокусных отношений;
- объемлющая эпюра;
- способы построения объемлющих эпюр.
Проверьте, как Вы умеете при расчете неразрезных балок:
- нумеровать опоры и пролёты;
- образовывать основную систему;
- составлять и решать уравнения трёх моментов;
- строить эпюры окончательных изгибающих моментов и поперечных сил;
- определять опорные реакции;
- строить эпюры окончательных изгибающих моментов и поперечных сил методом моментных фокусных отношений.
Проверьте, можете ли Вы вывести:
- уравнения трёх моментов при действии нагрузки;
- уравнения трёх моментов при действии осадки опор;
- формулы для вычисления фокусных отношений;
- формулы для расчёта неразрезной балки методом моментных фокусных отношений.
Проверьте, можете ли Вы обосновать:
- фокальные свойства неразрезной балки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.