di1 X1 + ... + dii X i + ... + din-1 X n-1 + DiP + Dic = 0
(i = 1,..., n -1)
(10.2)
Однако, как было выяснено в модуле М.8, трудоемкость составления и решения системы канонических уравнений может изменяться при исполь- зовании различных вариантов основной системы метода сил. Сделаем ана- лиз трудоемкости составления и решения системы уравнений (10.2) для двух вариантов основной системы.
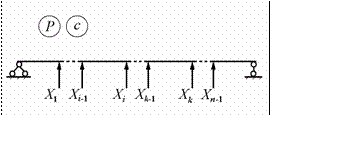 В качестве первого варианта основной системы
выберем простую балку, полученную из заданной системы удалением всех промежуточных
опор (рис.10.9)
В качестве первого варианта основной системы
выберем простую балку, полученную из заданной системы удалением всех промежуточных
опор (рис.10.9)
Рис.10.9
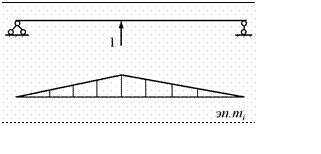 Рассмотрим два
произвольных единичных состояния №
i (рис.10.10)
Рассмотрим два
произвольных единичных состояния №
i (рис.10.10)
Рис.10.10
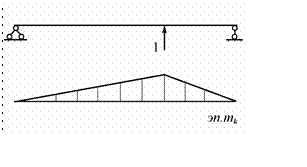 и номера k (рис.10.11)
и номера k (рис.10.11)
Рис.10.11
и изобразим качественное очертание единичных эпюр изгибающих момен- тов. Нетрудно увидеть, что при перемножении этих эпюр ни один из ко- эффициентов канонических уравнений (10.2) в ноль не обращается
dik ¹ 0
(i, k = 1,..., n -1).
Следовательно, вариант основной системы метода сил в виде простой балки не приносит никаких упрощений, как при составлении, так и при решении канонических уравнений (10.2).
В качестве
второго варианта основной системы выберем
многопролетную шарнирную
балку, полученную из заданной
системы введени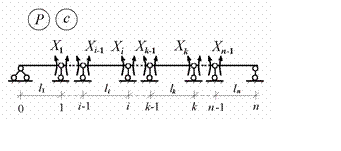 ем шарниров во все промежуточные опорные сечения (рис.10.12)
ем шарниров во все промежуточные опорные сечения (рис.10.12)
Рис.10.12
И здесь также рассмотрим два произвольных единичных состояния № i
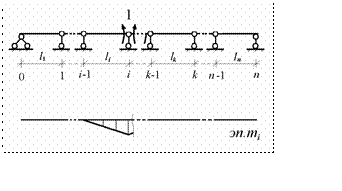 (рис.10.13)
(рис.10.13)
Рис.10.13
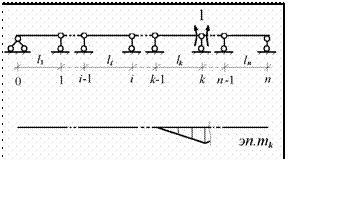 и номера k (рис.10.14)
и номера k (рис.10.14)
Рис.10.14
и тоже изобразим качественное очертание единичных эпюр изгибающих моментов. Нетрудно увидеть, что в этом случае все коэффициенты, у кото- рых модуль разности индексов больше единицы, обращаются в ноль
![]()
![]() dik = 0,
dik = 0,
i - k
> 1.
(10.3)
И только коэффициенты, для которых это условие не выполняется, отличны от нуля
![]()
![]() dik¹ 0,
dik¹ 0,
i- k
£ 1.
(10.4)
С учетом условий (10.3) и (10.4) канонические уравнения (10.2) принимают вид трехдиагональной ленточной системы уравнений
dii-1 X i-1 + diiX i+ dii+1 X i+1 + DiP+ Dic= 0
(i = 1,..., n-1)
(10.5)
Входящие в (10.5) основные неизвестные являются опорными моментами неразрезной балки, возникающими от действия нагрузки и осадки опор. Составление и решение уравнений (10.5) менее трудоемко по сравнению с исходными уравнениями (10.2).
Таким образом, для дальнейшего расчета неразрезной балки методом сил принимается второй вариант основной системы (рис.10.12).
11.2.2. Определение коэффициентов канонических уравнений
![]() Для определения коэффициентов канонических
уравнений (10.5) применяется формула Максвелла-Мора
для вычисления единичных пере- мещений, учитывающая
влияние только изгибных деформаций
Для определения коэффициентов канонических
уравнений (10.5) применяется формула Максвелла-Мора
для вычисления единичных пере- мещений, учитывающая
влияние только изгибных деформаций
dik
= å ò mi mk ds
(k = i -1, i, i +1). (10.6)
j s EI
Применение формулы
(10.6) связано с рассмотрением трех единичных со![]() стояний и построением единичных эпюр изгибающих моментов
стояний и построением единичных эпюр изгибающих моментов
mi -1 , mi , mi +1.
mi -1
Единичноесостояние
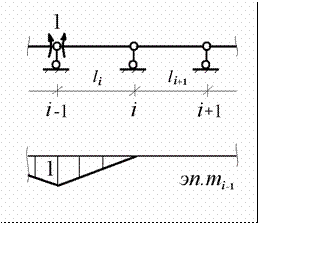 показаны на рис.
10.15
показаны на рис.
10.15
Xi -1
и соответствующая ему единичная эпюра
Рис.10.15
![]() Единичное состояние
Единичное состояние
mi показаны на рис. 10.16
Xi и соответствующая ему единичная эпюра
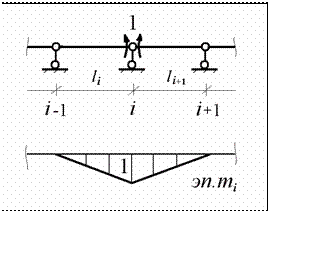 Рис.10.16
Рис.10.16
mi +1
Единичноесостояние
![]()
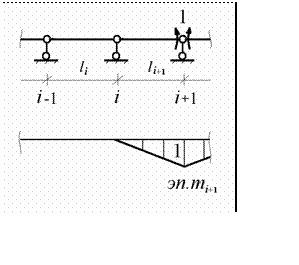 показаны на рис. 10.17
показаны на рис. 10.17
X i +1
и соответствующая ему единичная эпюра
Рис.10.17
Перемножая по правилу Верещагина единичные эпюры найдем побочный коэффициент
mi -1
и mi ,
![]()
|
dii -1 =
. (10.7)
6 (EI)i
Перемножая по правилу Верещагина единичную эпюру mi
себя, найдем главный коэффициент
саму на
|
|
![]()
![]()
![]() d = ⎜ i
d = ⎜ i
+ li +1
⎞
⎟ . (10.8)
ii 3 ⎜ (EI) (EI) ⎟
⎝ i i +1 ⎠
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.