Расчет неразрезных балок, страница 3

Перемножая  по  правилу  Верещагина  единичные  эпюры найдем побочный коэффициент

mi +1

и  mi ,

1

dii +1  =

li +1

.                                   (10.9)

6 (EI )i +1

Из  полученных  формул  (10.7)-(10.9)  следует,  что  для  определения коэффициентов канонических уравнений метода сил при расчете неразрез- ной балки согласно принятому варианту основной системы (Рис.10.12) не нужно каждый раз строить и перемножать единичные эпюры изгибающих моментов. Для их определения достаточно в полученные конечные формулы  подставить  геометрические  и  жесткостные  параметры  соответствующих пролетов неразрезной балки.

10.2.3. Определение свободных членов канонических уравнений

Канонические уравнения (10.5) содержат свободные члены, связанные с действием нагрузки и осадки опор.

Свободные  члены,  связанные  с  действием  нагрузки,  являются  перемещениями, возникающими в основной системе по направлению основных неизвестных. Поэтому они определяются по формуле Максвелла-Мора для определения перемещений от нагрузки с учетом влияния только изгибных деформаций

DiP

= å ò mi M P ds

(i = 1,..., n -1).                        (10.10)

j   s    EI

Применение  формулы  (10.10)  связано  с  использованием  ранее  построен-

ной единичной эпюры изгибающих моментов  mi

(рис.10.16), а также  свя-

зано с рассмотрением грузового состояния и построением грузовой эпюры

изгибающих моментов

MP .

Грузовое  состояние  при  действии  нагрузки  произвольного  вида  и

соответствующая ему грузовая эпюра  M P

в двух пролетах основной сис-

темы, смежных с опорой i , показаны на рис. 10.18

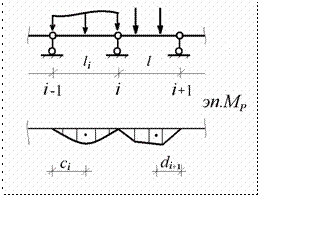
Рис.10.18

Будем  считать,  что  для  грузовой  эпюры  в  пролетах  известны  величины

площадей

wi,

wi+1

и расстояния от центров тяжестей фигур эпюр до край-

них опор ci,

di+1 .

Перемножая  по правилу  Верещагина  единичную  эпюру  mi

с  грузо-

вой эпюрой

MP, найдем свободный член от нагрузки

=   1

(EI)i

A1

li(EI)i+1

B

i+1

li+1

,                                   (10.11)

i     = wi ci ,

Si +1  = wi +1di +1

- статические моменты участков грузовой эпюры

i и i+1 пролетов, соответственно, относительно левой и правой опор этих пролетов. Левая опора условно обозначена символом A , правая – симво- лом B.

Из  полученной  формулы  (10.11)  следует,  что  для  определения  сво- бодных членов от нагрузки канонических уравнений метода сил при рас- чете  неразрезной  балки  согласно  принятому  варианту  основной  системы

(рис.10.12)  не  нужно  каждый  раз  перемножать  единичные  и  грузовую эпюры изгибающих моментов. Для их определения достаточно в получен- ные конечные формул подставить геометрические и жесткостные параметры соответствующих пролетов неразрезной балки, а также параметры грузовой эпюры в этих пролетах.

Свободные члены, связанные с действием осадки опор, являются пе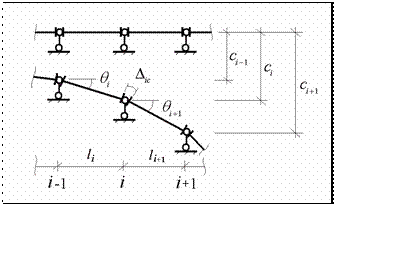ремещениями, возникающими в основной системе по направлению основных  неизвестных,  и  представляют  собой  взаимные  углы  поворота  торцов на промежуточных опорах. Тогда из рис.10.19

Рис.10.19

следует, что произвольный свободный член номера i определяется по формуле

Dic   = qi +1  - qi

(i = 1,...,n - 1)

.                                   (10.12)

i +1   и q

углы поворота пролетов основной системы, примыкающих