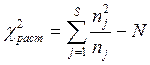Проектирование системы профилактики АТС, обеспечивающей безопасность дорожного движения (на примере Ширинского района), страница 8

                                     (16)

В нашем примере, результаты расчета удовлетворяют неравенству χ²_{расчетное} = 2,8 >χ²_{табличное}= 11,345. В этом случае гипотеза подтверждается т.к выполняется условие .

4 Оценка количественных характеристик безотказности и долговечности

4.1Оценка вероятности безотказной работы

Согласно ГОСТ 27.002 – 83 вероятность безотказной работы P(L) есть вероятность того, что в пределах заданной наработки на отказ элемента АТС не возникнет. Статистически определяется по  приближенной формуле:

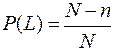                      ,                                                        (17)

где     n – количество отказавших элементов за пробег от 0 до L;

N – Общее количечество элементов, находящихся под наблюдением.

Известно, что вероятность безотказной работы и вероятность отказа составляют полную группу событий:

                    P (L) +F (L) =1                                            (18)

По закону Вейбулла-Гнеденко 

                                                               (19)

По нормальному закону 

                     P(L)=1 – Ф(z),                                            (20)

где  

Интервальную оценку  определяют, подставив соответственно  и  (или  и  ).

произведем расчет вероятности безотказной работы по закону Вейбула – Гнеденко. Полученные данные занесем в таблицу 2. По данным таблицы построим графики вероятности безотказной работы от пробега.

Таблица 2 – Вероятность безотказной работы

L,тыс км	Р(L)в	Р(L)ср	Р(L)н
0	1	1	1
10	0,986	0,9809	0,972
20	0,933	0,9093	0,870
30	0,838	0,7850	0,702
40	0,710	0,62507	0,504
50	0,565	0,45561	0,318
60	0,419	0,30211	0,174
70	0,2894	0,18124	0,0830
80	0,185	0,09789	0,033837
90	0,109	0,04740	0,0117
100	0,059	0,02049	0,003465
110	0,0297	0,00788	0,00086
120	0,013	0,00268	0,00017

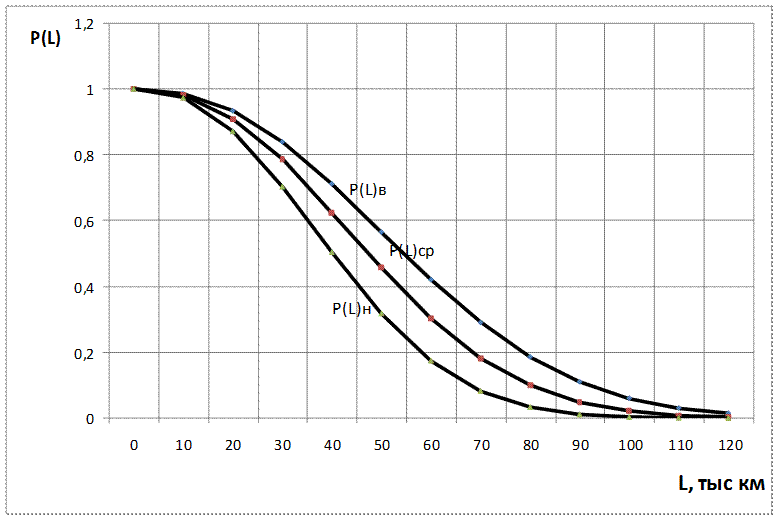
Рисунок 1 – График вероятности безотказной работы до первой замены

4.2 Оценка интенсивности отказов элемента АТС, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник. Статистически оценивается по приближенной формуле:

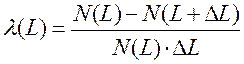                   ,                                      (21)

Где  N(L)=(N-n) – количество работоспособных элементов при пробеге L.

Для закона Вейбулла-Гнеденко его точечная оценка, отказ, тыс.км.,

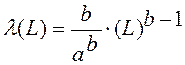                                                                             (22)

Интервальную оценку [ определяют при подстановке  вместо в формулу (21) вместо а значений  и

Для нормального закона

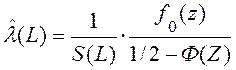                                                           (23)

Рассчитаем таблицу и построим кривые

4.3Оценка плотности распределения отказов

Плотность распределения отказов f(L), тыс.км^-1, - это плотность вероятности того , что наработка элемента АТС до отказа окажется меньше L. Статически оценивается по формуле

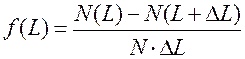                                                                             (24)

Для закона Вейбулла-Гнеденко

               

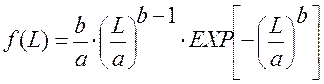
В случае нормального закона распределения

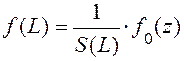                                                                              (25)

Рассчитаем таблицу и построим кривую f(L)

Таблица 3 – Точечная оценка интенсивности отказов