Проектирование системы профилактики АТС, обеспечивающей безопасность дорожного движения (на примере Ширинского района), страница 12

Метод предусматривает первые N восстановлений, что дает приблизительную оценку функции восстановления и параметра потока отказов. В данном случае для практики технической эксплуатации автомобилей такое допущение уместно, хотя погрешности графических построений не позволяют добиться большей точности. Метод прост и доступен для практического применения, при решении инженерных задач технической эксплуатации автомобилей, например при оценке потребности запасных частях по интервалам наработки.

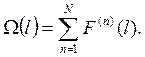                                                           (37)

Параметр потока отказов определяется по формуле:

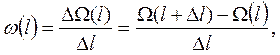                                        (38)

где Δl – интервал наработки, величина которого выбирается как можно меньшей исходя из размеров графика. Чем меньше Δl, тем выше точность расчета параметра потока отказов, но ниже точность графических построений.

Метод использует общие свойства композиции распределений, принимая за математическое ожидание оценку средней наработки

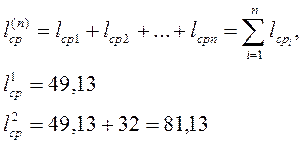                         (39)

а за дисперсию – квадрат оценку среднего квадратичного отклонения

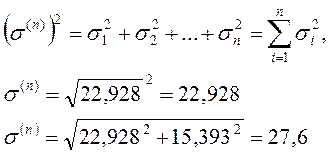                                       (40)

С помощью этого метода можно выполнять аналитический расчет функций композиции распределения; графическое построение ведущей функции как суммы ординат функции композиции; расчет параметра потоков отказов графическим дифференцированием кривой ведущей функции.

Расчет функций композиции распределения наработок до замен двигателя

Таблица 12 – Расчет функции композиции распределения наработок до замен

α	Uр	F1	F2
		l¹ср±Uр٭σ¹к	l²ср±Uр٭σ²к
0,1	-1,282	19,736304	45,7468
0,2	-0,842	29,824624	57,8908
0,3	-0,524	37,115728	66,6676
0,4	-0,253	43,329216	74,1472
0,5	0	49,13	81,13
0,6	0,253	54,930784	88,1128
0,7	0,524	61,144272	95,5924
0,8	0,842	68,435376	104,3692
0,9	1,282	78,523696	116,5132

Таблица 13 – Определения ведущей функции

Таблица 14 - Определение параметра потока восстановления

L,тыс км	ΔL	(L)	Ω(L+ΔL)	W отказ/тыс. км
0	10	0	0,05	0,005
10	10	0,05	0,1	0,005
20	10	0,10	0,20	0,01
30	10	0,20	0,34	0,014
40	10	0,34	0,62	0,028
50	10	0,62	0,90	0,028
60	10	0,90	1,16	0,026
70	10	1,16	1,38	0,022
80	10	1,38	1,55	0,0165

Все три  системы координат располагают одну под другой так, чтобы ординаты находились на одной линии, а масштабы по оси наработки были одинаковы. (рис.10)

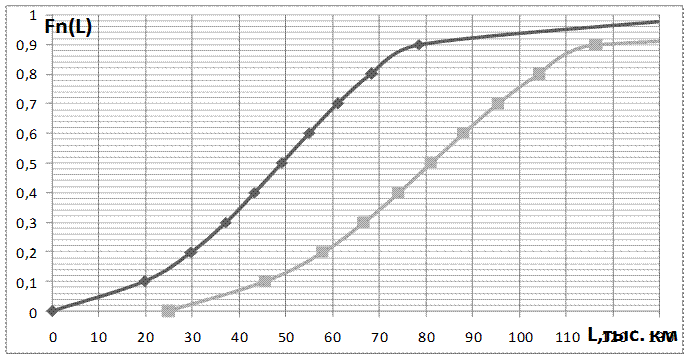
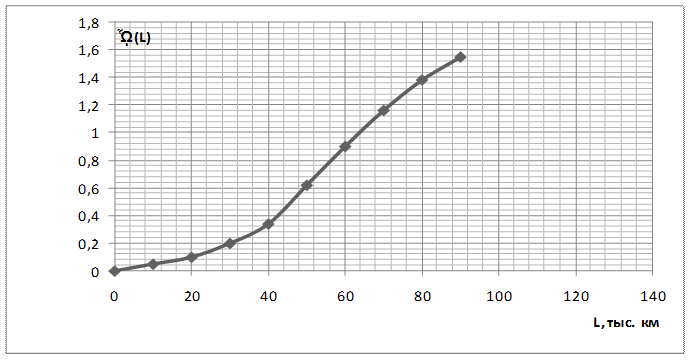
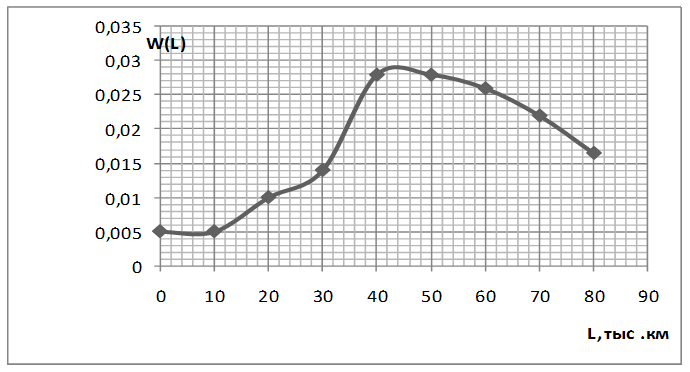
Рисунок 10 - Графоаналитический метод расчета характеристик процесса восстановления F⁽ⁿ⁾, Ω(l) и ω(l).

Первая система координат (рис.1) состоит из  совмещенных графиков функции распределения  F⁽¹⁾(l)=F(l) наработки до первого восстановления и распределения наработок до последующих восстановлений F⁽²⁾(l), F⁽³⁾(l)  и т.д.

Исходными данными для построения кривых F⁽ⁿ⁾(l) являются средние наработки между восстановлениями l_срi и среднее квадратические отклонения σ_i, что позволяет рассчитать l_ср⁽ⁿ⁾ и σ⁽ⁿ⁾ по состояниям.