Проектирование системы профилактики АТС, обеспечивающей безопасность дорожного движения (на примере Ширинского района), страница 7

35 22 27 61 62 31 32 38 41 455 47 49 53 58 59 65 68 70 75 24 26 72 78 82 85 95 14 19 20 21

Количество членов вариационного ряда N=30

Выборочная средняя, тыс.км:

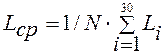                                                   (1)

Дисперсия (несмещенная), (тыс.км)²,

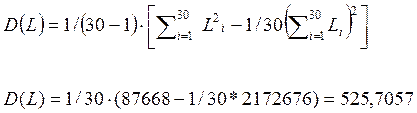
Среднее квадратическое отклонение, тыс.км:

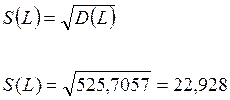                                         (2)

Коэффициент вариации:

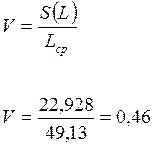                                                     (3)

2.1 Интервальная оценка

Для расчета вначале определим предельной относительной ошибки при =0,90, для чего надо рассчитать уровень значимости  и выбрать из табл.1 приложение 2[31] значение .

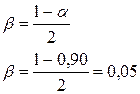                                                        (4)

в =2,3061

( 60)= 43,188

Расчетное значение предельной относительной ошибки

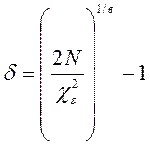                                                       (5)

=(2*30/43,188)^1/2,3061 -1 =0,15

С вероятностью  можно утверждать, что средняя наработка до замены рассматриваемого элемента ТС находится в интервале , что и является интервальной оценкой.

Границы доверительного интервала, тыс.км:

                                                       (6)

Lсрн = 49,13*(1-0,15)= 41,765

Lсрв = 49,13*(1+0,15)= 56,49

Lср = 49,13

Значение гамма-функции определим из таблицы 4[31] в зависимости от полученного значения коэффициента вариации:

= 0,8859

2.3 Оценка параметра масштаба закона Вейбулла-Гнеденко

Точечная оценка параметра масштаба закона Вейбулла-Гнеденко, тыс.км:

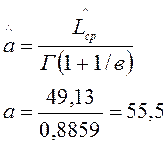                                                   (7)

Значение гамма-функции определим из таблицы 4[31] в зависимости от полученного значения коэффициента вариации:

= 0,8859

Граничные значения интервальной оценки, тыс.км:

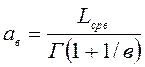                                                                (8)

а_в=56,49/0,8859=63,77

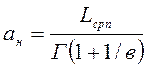                                                                (9)

a_н =41,765/0,8859=47,14

 

3. Проверка нулевой гипотезы

χ²_рас < χ²_табл(β,k) – условие соблюдение нулевой гипотезы, где     χ²_рас – значение критерия согласия Пирсона, вычисленное по эксперимен- тальным данным; χ²_табл – критическая точка критерия ( по таблице № 6 [31] );

где     β – уровень значимости, k – число степеней свободы,

β = 0,1; где S – количество частных интервалов выборки,

r – количество параметров предлагаемого распределения,

r = 2.

Количество интервалов S по правилу Штюргеса:

                                              (10)

k = S – l – r,          k = 6-1-2=3;

Табличное значение критерия          (0.10;3)=11,345 (таблица №2,) [31].

Протяжённость интервала(тыс.км.):

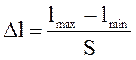                                              (11)

                                                        

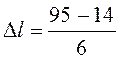
где L_max – наибольший элемент L_min – наименьший элемент;\

- границы интервалов определяют по формуле

                                                (12)

где j=1, 2, …, s.

Расчёт теоретических частот

                                            (13)                                                                                           

                                                                                      (14)

где F(L_j) – функция распределения отказов;

ΔF(L_i) = F(L_i+1) - F(L_i).                               (15)

Значит  равно:

=30 * 0,17 = 5,39

= 30 * 0,21 = 6,38

= 30 * 0,22 = 6,75

= 30 * 0,18 = 5,42

= 30 * 0,11 = 3,41

= 30 * 0, 09 =2,7

Таблица 1- Расчет - распределения согласия Пирсона

							/
1	0	27,5	8	64	0,18	5,39	11,8
2	27,5	41	5	25	0,27	6,38	3,9
3	41	54,5	4	16	0,22	6,75	2,4
4	54,5	68	6	36	0,18	5,42	6,64
5	68	81,5	4	16	0,11	3,41	1,17
6	81,5	∞	3	9	0,09	2,7	3,3