Повышение надёжности электроснабжения потребителей 10-15 кВ Каскада Свирских ГЭС, страница 14

Для   случаев   моделирования   системы    самовозбуждения   без   последовательных   трансформаторов,   когда   напряжение,   приложенное   к  обмотке   возбуждения,   пропорционально     U_Г.,   в   модели,   предусмотрена   возможность   коррекции   ЭДС   по   выражению:

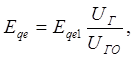                                                                                                                                             (2.35)

где   E_{qe1 –} величина,   соответствующая   напряжению  возбуждения   при   U_Г=U_Г0.   Без   учёта   такой  зависимости   Е_qe    от   U_Г.   расчёты   переходных   процессов   с   генераторами,   имеющими   систему   самовозбуждения   без   последовательных   трансформаторов,   могут   оказаться   неправильными.   При   независимой   системе   возбуждения   или   при   самовозбуждении   с   последовательными   трансформаторами   E_qe=E_qe1.     Модель   бесщёточной   системы    возбуждения   отличается    от   рассмотренной   только   параметрами.

Такая   же   структура   модели   используется   и   для   других   систем   возбуждения.    В   модели    высокочастотной   системы   возбуждения   первый   сумматор,   ограничитель   и   апериодическое  звено   с    постоянной   времени    Т_р.в   соответствуют   корректору   напряжения    (Т_р.в≈1с),   причём   имеется   возможность   учесть   зависимость   уставки   АРВ   по   напряжению   U_Г0   от   частоты    ω.   В   модели   возбудителя,   имеющего   компаундирующую   обмотку,   что   соответствует   жёсткой   положительной   обратной   связи   по   току   ротора,   в   сумматор   ∑₂     введена   величина     i_f – i_f0.    Приближённое   моделирование    блока   сильной   стабилизации   (БСС)   в   высокочастотной   системе   возбуждения   осуществлено   таким   образом,   что    постоянная   времени   возбудителя   Т_в   увеличивается   в   К_Тв   раз,   если   скорость   изменения   u_f,   пропорциональна   dE_qe/dt,      превышает   некоторое   пороговое   значение.

Структура   модели   электромашинной   системы    возбуждения   с   корректором   напряжения   и   компаундированием   отличается   от  приведённой  тем,   что   в     вместо   слагаемого   i_f ─ i_f0  введены :  слагаемое I_Г –I_Г0  ( с  соответствующим   коэффициентом   усиления),  моделирующее  компаундирование ,   и   слагаемое ,  моделирующее   релейную   форсировку  возбуждения    с   учётом   запаздывания    и   коэффициента   возврата.   В   модели    форсировки   возбуждения    предусмотрена    возможность   изменять    постоянную   времени    возбудителя Т_В ,   что    имеет   место ,    например ,   при   шунтировании    резистора   в    обмотке     возбуждения     возбудителя.

При   расчетах     переходных    процессов    иногда    возникает    необходимость    моделирования    различных    отказов    в    системе   возбуждения ,    например    выхода    её   из    работы   (E_qe= 0).  Такие   задачи    приходится    решать    для    анализа    режима    энергосистемы    в    случаях     потери    возбуждения    какого-либо   генератора    или    для    анализа    происшедшей    аварии,   связанной    с    неполадками    в    системе    возбуждения.   Подготовка    и    осуществление   таких     расчетов   облегчаются ,   если    в    модели    системы    возбуждения    в    сумматорах     и   предусмотрены      дополнительные   слагаемые,   значения    которых    можно    изменять   во    времени.  Управление    величиной   E^mak_qe  полезно   также    и    для    моделирования   действия   ограничителя    перегрузки   обмотки   возбуждения   (ОП) у   генераторов   с   форсированным    охлаждением.   Действию   ОП    соответствует   снижение   E^mak_qe  до   значения,    примерно   равного    (0,9÷ 0,95)  Е_{q ном} .  Выдержка    времени    ОП   определяется    фактической   перегрузкой    обмотки    возбуждения .   При   i_f=2i_fном  срабатывание   ОП   происходит   через  10-20с.

2.4.  Модель   нагрузки

При    расчете   переходного   процесса   нагрузка   может   учитываться:

1) постоянной   проводимостью;