Математическое моделирование экономических процессов на железнодорожном транспорте, страница 23

Нужно знать откуда какая цифра берется

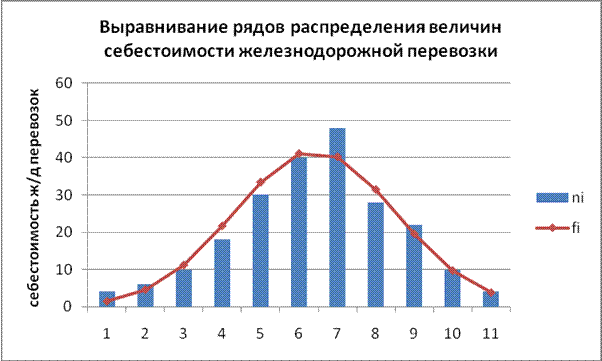
Сумма найденных теоретических частот f_i = 218,29 сравнивается с суммой частот эмпирического распределения n_i = 220. Эти суммы различаются незначительно (220 – 218,29 = 1,71), поскольку расхождение фактического распределения с теоретической нормальной кривой распределения носит случайный характер, то гипотеза соответствия экспериментального распределения теоретическому принимается.

В практике статистических расчетов для оценки правомерности гипотезы соответствия фактического распределения нормальному принят критерий "хи-квадрат" иначе говоря, критерий Пирсона:

По полученным расчетам величина критерия Пирсона  χ² = 7,74.

После определения величины критерия Пирсона рассчитывается число степеней свободы:

r = k – 3

где k - число интервалов в фактическом распределении.

В данном примере  r = 11 – 3 = 8.

При заданном уровне значимости 5% предусматривающем 5% ошибку и количестве степеней свободы, равном 8, определяется табличная величина критерия Пирсона, χ ² = 15,5.

Найденное в расчетах значение меньше табличного, поэтому гипотеза о соответствии эмпирического распределения теоретическому принимается: χ² = 7,74 < 15,5.

2.4. Прогнозирование экономических показателей методом простого экспоненциаьного сглаживания

Задание 1: Рассчитать заданным методом прогноз для локомотивного депо на 10-ый год при параметрах сглаживания a=0.3, a=0.5.Данные вариантов по динамике изменения величин экономических показателей работы локомотивного депо приведены ниже в таблице.

Таблица № 4

Динамика изменения средней заработной платы

Год	Средняя заработная плата, тыс. руб.	Yt - прогноз1	Yt - прогноз2
1	1680	-	-
2	1700	1686	1690
3	1740	1712	1720
4	1740	1740	1740
5	1780	1752	1760
6	1780	1780	1780
7	1800	1786	1790
8	1820	1806	1810
9	1860	1832	1840
10	1860	1860	1860

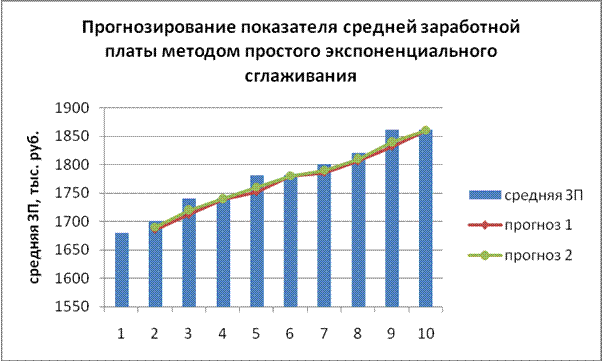
Взвешенная скользящая средняя с экспоненциально распределенными весами характеризует в основном значение процесса на конце интервала сглаживания. Это свойство используется для прогнозирования.

где Y_t – значение прогнозируемого показателя в точке t;

Y_t-1 -- значение прогнозируемого показателя в точке t-1;

y_t – фактическое значение показателя в точке t;

α – фактор затухания, константа (коэффициент) сглаживания.

Для константы сглаживания – фактора затухания – наиболее подходящим является значение 0,3 . Это значение показывает, что ошибка текущего прогноза установлена на уровне 30% ошибки предыдущего прогноза. Значение константы сглаживания равное 0,5 показывает, что ошибка текущего прогноза установлена на уровне 50% ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к сдвигу аргумента для предсказанных значений. По величине константы сглаживания определяем, насколько сильно влияют на прогнозы погрешности в предыдущем прогнозе.

Данные второго прогноза более близки к предсказанным значениям, нежели данные первого прогноза. Это видно из построенного графика.

3. Общая задача линейного программирования это обязательно нужно!!!!!

Имеется возможность выпуска 4 видов продукции (N1, N2, N3, N4) на пяти  типах машин (A, B, C, D, E).

1.  Сформировать математическое описание задачи.

2.  Построить каноническую форму.

3.  Найти оптимальный план.

4.  Выполнить анализ отимального производственного плана, включая состав и объем выпуска продукции, получаемую при этом прибыль, эффективность и состояние использованных ресурсов.