![]() (23)
(23)
Поскольку каждый столбец полной матрицы соединений Аа содержит необходимую информацию о концевых узлах каждой ветви и её ориентации, то последовательным скалярным умножением этих столбцов на один и тот же вектор узловых давлений Р получим соотношения (23) в компактной форме сразу для всей схемы
![]() .
(24)
.
(24)
Математическая модель метода узловых давлений сводится к системе уравнений:
![]() ;
;
![]() ;
(25)
;
(25)
![]() , которая состоит из m
– 1 +2n
уравнений относительно векторов
, которая состоит из m
– 1 +2n
уравнений относительно векторов ![]() , DР и m-1 значений Pi для линейно независимых
узлов. Здесь также может быть исключен вектор DР, что
сократит (24) до:
, DР и m-1 значений Pi для линейно независимых
узлов. Здесь также может быть исключен вектор DР, что
сократит (24) до:
![]() ;
; ![]() .
(26)
.
(26)
Система (26) является исходной в МД.
Метод узловых давлений в отличие от метода контурных расходов можно применять для гидравлических цепей с любой топологией. Одно из важных достоинств МД - относительная простота программы формирования уравнений гидравлической цепи с помощью ЭВМ. Матрица соединений имеет очень простой вид. Она задает связь узлов и ветвей цепи и тем самым непосредственно описывает её топологию. Действия над матрицами (транспонирование, суммирование, перемножение) легко программируются. Кроме того, в инженерных задачах узловые давления задаются часто в явном виде, что делает более удобными МД.
Вместе с тем следует отметить, что не существует каких-либо привилегированных методов, заведомо более эффективных и гарантирующих быстрое получение результата при любых возможных сочетаниях исходных данных. Каждый метод имеет свою область предпочтительного применения, не говоря уже о том, что критерии практической и вычислительной эффективности весьма разнообразны и зачастую противоположны по своим требованиям.
7. Основные методы решения и алгоритмы программ
Методы решения систем уравнений (22) и (26) можно разделить на две основные группы: вариационные и линеаризации. Последние исследования показали, что методы линеаризации требуют меньших затрат машинного времени, чем вариационные.
Базисным для МНР и МД является модифицированный метод линеаризации Ньютона (Ньютона-Рафсона) /1/, предназначенный при соблюдении условий сходимости для решения систем нелинейных уравнений самого общего вида:
![]() (27)
(27)
где Х=[X1, X2, …, Xn]- вектор аргументов; F=[F1, F2, …, Fn]- вектор функция.
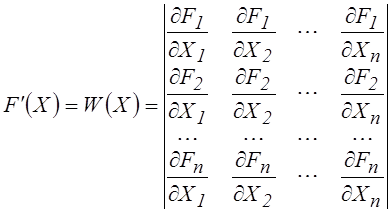 .
.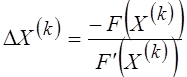 .
.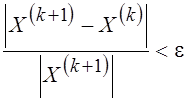
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.