Основы гидравлического расчета трубопроводных систем на ЭВМ: Методические указания к практическим занятиям по курсам “Проектирование, монтаж и испытание судовых систем” и “Производство и распределение энергоносителей промышленных предприятий”, страница 5

Полное описание структуры ориентированного графа дает m´n - матрица соединений (инциденций), m строк которой являются порядковыми номерами узлов j, а n столбцов - номерами ветвей i. Числа узлов j и ветвей i являются параметрами гидравлической цепи. Элементами a_ij этой матрицы являются символы наличия или отсутствия ветви  i, присоединенной к узлу j, которые принимаются a_ij=+1 - для выходящей из узла ветви; a_ij= -1 - для входящей в узел ветви и a_ij= 0, если ветвь не связана с узлом. Для графа цепи на рис.1,б получим полную матрицу соединений (инциденций):

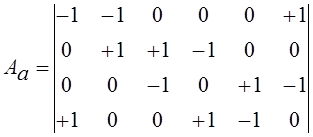                                      (9)

Так как каждая ветвь соединяет два узла (выходит из одного узла и входит в другой), то столбец матрицы состоит из двух нулевых элементов + 1, - 1.

Для трех узлов цепи, показанной на рис.1,а, уравнения первого закона Кирхгофа приведены ниже:

узел 1                                   -V₁ -V₂ +V₆ = 0;

узел 2                                   V₂ +V₃ -V₄ = 0;                                               (10)

узел 3                                  -V₃ +V₅ -V₆= 0.

Сумма трех уравнений (10) является уравнением первого закона Кирхгофа для узла 4: -V₁ -V₄ +V₅ = 0. Нетрудно показать, что приведенные уравнения могут служить примером линейной зависимости уравнений первого закона Кирхгофа для четырех узлов (одно из четырех уравнений является следствием трех остальных). В общем случае, для цепи состоящей из m узлов, линейно независимы уравнения для m - 1 узлов. Таким образом, полное описание структуры ориентированного графа цепи можно получить с помощью, редуцированной матрицы соединений А. Эту независимую матрицу можно получить из полной матрицы А_авычеркиванием строки, соответствующей выбранному базисному узлу.

Приняв в качестве базисного узел 4 и соответственно вычеркивая четвертую строку в (9), получим редуцированную матрицу соединений:

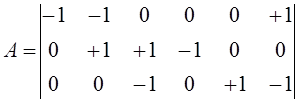                                 (11)

Если ввести вектор расходов  n  ветвей:

,

( т - знак транспонирования), то систему линейно-независимых уравнений первого закона Кирхгофа в m – 1 узлах в соответствии со смыслом матрицы  А можно записать в матричной форме сразу для всей цепи:

,                                                     (12)

где  - нулевой вектор размерности n.

Коэффициенты системы уравнений (10) для графа цепи на рис.1,б являются элементами матрицы соединений (11). Каждая строка системы (12) является уравнением первого закона Кирхгофа в  j^-ом узле:

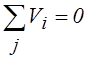
В общем случае, кроме расходов по всем ветвям, имеющим общий узел j, может быть задан узловой расход U_j.  (потребитель U_j>0 , если в узле j находится сток; приток U_j<0 если речь идет об источнике; U_j=0, если данный узел является простой точкой разветвления потоков в схеме). Уравнение первого закона Кирхгофа в j - м узле будет иметь вид:

, а для всей схемы в матричной форме:

,                                                 (13)

где   - вектор узловых расходов. Значения должны быть заданы таким образом, чтобы имел место их общий нулевой баланс по всем узлам схемы.

При анализе гидравлических цепей используют такие важные подграфы, как сечение, контур и дёрево графа.

Сечением называют множество ветвей, удаление которых разбивает граф на два несвязных подграфа, каждый из которых является связным. При этом присоединение любой из удаленных ветвей должно приводить к связному графу. На рис.4,а ветви графа, пересекающие k-ую линию (след замкнутой поверхности), образуют сечение, перечислим ветви образующие некоторые из сечений: а - I, 2, 6; в - I, 2, 3, 5; с –1, 3, 4, 6; д - 3, 5, 6 и т.д.

Разрыв указанных, ветвей разделяет граф на два подграфа с числами узлов m₁ и m₂= m - m₁. При m₁ = 1 состоит только из одного узла и ветви, сходящиеся к узлу, образуют сечение. Число возможных сечений может намного  превысить число узлов.