Матрица Q показывает, какие ветви входят в каждое из главных сечений. Для главных сечений графа на рис.5,а можно записать матрицу сечений:
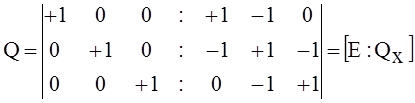 . (14)
. (14)
Матрица Q разбивается на две части: единичную матрицу Е порядка nд и подматрицу Qх порядка nд´nх, которая получается из матрицы главных сечений исключением всех ветвей дерева. Строка Qх показывает, какие хорды входят в сечение, образованное соответствующей ветвью дерева, а столбец - в какие главные сечения входит хорда.
Составление матрицы Q равносильно записи по первому закону Кирхгофа независимых уравнением расходов в главных сечениях - элементы матрицы являются коэффициентами уравнений, которые записываются суммированием расходов ветвей сечений. Для сечений графа на рис.5,а имеем:
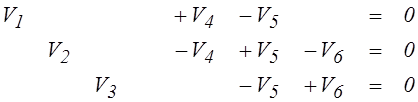
Коэффициенты этой системы являются элементами матрицы Q. С учетом (14) система уравнений для расходов сечений в матричной форме записывается в виде:
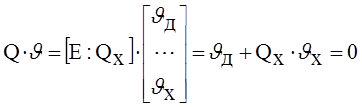 (15)
(15)
Здесь вектор расходов ветвей:
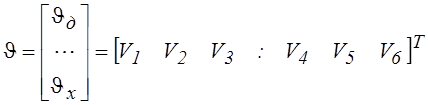 , где
, где ![]() ,
, ![]() - векторы расходов ветвей дерева и хорд.
Каждая строка в системе (15) является уравнением обобщенной формулировки первого
закона Кирхгофа одного из главных сечений k=(1…n):
- векторы расходов ветвей дерева и хорд.
Каждая строка в системе (15) является уравнением обобщенной формулировки первого
закона Кирхгофа одного из главных сечений k=(1…n):
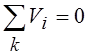
В каждое уравнение входит единственный расход ветви дерева. Поэтому систему (15) всегда можно решить относительно расходов всех ветвей дерева, выразив их через расходы хорд:
![]() (16)
(16)
Для рассматриваемой гидравлической цепи вектор расходов ветвей дерева:
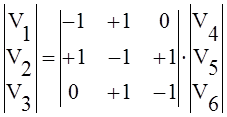
Каждой хорде можно приписать единственный (базисный) контур, который состоит из одной хорды и нескольких ветвей дерева. При этом эта хорда не входит в другие главные контуры, поэтому уравнение второго закона Кирхгофа для главных контуров будут независимыми. Число главных контуров равно числу хорд: см. уравнение (14). На рис.5,б показаны три главных контура, соответствующих выбранному дереву.
Матрица главных (базисных) контуров, описывающая соединения ветвей, входящих в независимые главные контуры имеет n столбцов и столько строк, сколько контуров имеется в графе. При этом порядковые номера контуров совпадают с номерами хорд. Элементы матрицы равны +1 при совпадении, -1 при несовпадении направления ветви с направлением обхода контура и 0, если ветвь не входит в контур. Направление обхода контура выбирается таким образом, чтобы ему соответствовала ориентация хорды.
Для графа на рис.5,б матрица главных контуров имеет вид:
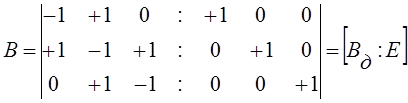 . (17)
. (17)
Матрица В разбивается на две части: подматрицу Вд порядка nх´nд и единичную матрицу Е порядка nх. Строка Вд показывает, какие ветви дерева входят в контур, образованный замыканием соответствующей хорды, а столбец – в какие главные контуры входит ветвь дерева.
Составление матрицы В равносильно записи в соответствии со вторым законом Кирхгофа независимых уравнений потерь напора в главных контурах. Элементы матрицы являются коэффициентами уравнений, которые можно записать, суммируя потери давления в ветвях контуров (см.рис.5,б):
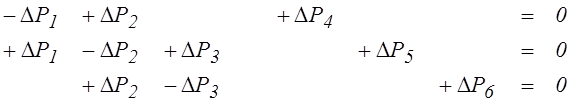
С учетом матрицы (17), получим компактную запись второго закона Кирхгофа для всей цепи:
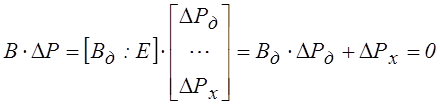 (18)
(18)
Здесь вектор потерь напора ветвей:
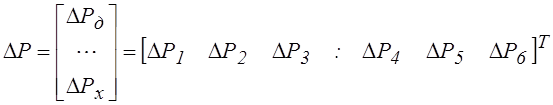 , где DРд,DРх - векторы потерь напора
ветвей дерева и хорд. Каждая строка в системе (18) является уравнением второго
закона Кирхгофа одного из главных контуров с=(1…nx):
, где DРд,DРх - векторы потерь напора
ветвей дерева и хорд. Каждая строка в системе (18) является уравнением второго
закона Кирхгофа одного из главных контуров с=(1…nx):
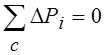
входит единственная потеря напора хорды. Систему (18) можно решить относительно потерь давлёния всех хорд, выразив их через потери давления ветвей дерева:
![]() .
.
Для рассматриваемой гидравлической цепи вектор потерь напора хорд:
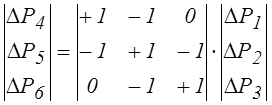
Матрицы главных сечений и главных контуров связаны между собой - входящие в них матрицы Qx и Bд определяют друг друга. Для графа на рис.5 имеем:
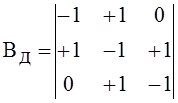 ;
; 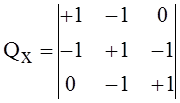
Номера, строк и столбцов Qx являются соответственно номерами столбцов и строк Bд. Поэтому вторая матрица равна транспонированной первой матрице с обратным знаком:
![]()
Связь между матрицами Qx и Bд, а следовательно между матрицами Q и В является следствием того, что выбранное дерево однозначно определяет как главные контуры, так и главные сечения. Из (16) и (17) при учете (18) имеем:
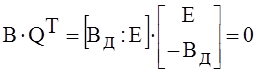 ;
; 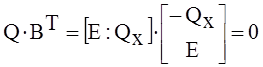
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.