Основы гидравлического расчета трубопроводных систем на ЭВМ: Методические указания к практическим занятиям по курсам “Проектирование, монтаж и испытание судовых систем” и “Производство и распределение энергоносителей промышленных предприятий”, страница 4

Все дуги, имеющие одну пару начальных и конечных вершин, называются параллельными. Дуга называется петлей, если инцидентная вершина j является одновременно начальной и конечной ее вершиной. Граф без петель и параллельных дуг называется простым. Для того, чтобы включить в структурную графовую модель неструктурную (качественную) информацию, довольно часто каждому ребру (или каждой вершине) рассматриваемого графа приписывают некоторый вес. Граф, ребрам (или  вершинам) которого приписаны веса, называется взвешенным.

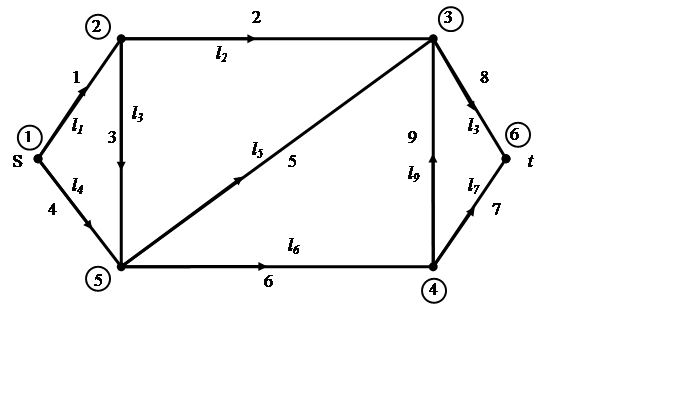
Графы являются удобным средством моделирования различных транспортных сетей, в том числе и трубопроводных сетей, когда изучается структура сети, возможности ее функционирования. Транспортная ceть есть ориентированный взвешенный граф, который не имеет петель и удовлетворяет следующим условиям:                   

1)  Существует только одна вершина с нулевой полустепенью захода (d^-(j)=0). Эта вершина называется источником и обозначается через S.

2)  Существует только одна вершина с нулевой полустепенью исхода (d⁺(j)=0). Эта вершина называется стоком и обозначается через t.

Пример транспортной сети представлен на рис.2. Рядом с каждой дугой l_i  приведен её вес.

Рис.2. Транспортная сеть

В теории гидравлических цепей используется терминология на стыке смежных дисциплин (теории электрических цепей, линейной алгебры, теории графов и гидравлики). При этом предпочтение отдается техническим терминам, как более наглядным и привычным, например, «ветвь» и «участок», а не «ребро» или «дуга», «узел» вместо «вершины».

Пo этой причине далее в тексте при рассмотрении необходимых понятий из теории графов использована терминология гидравлики.

С точки зрения теории графов расчетная схема гидравлической цепи -  взвешенный ориентированный граф; т.е. совокупность трех упорядоченных множеств: множества узлов; множества ветвей; множества условных знаков характеризующих количественные параметры гидравлической цепи. Среди количественных параметров гидравлической цепи, которые задаются в виде веса ветвей и узлов, различают: технические характеристики - диаметр, длина и т.п.; гидравлические параметры - расходы в узлах или ветвях, давления в узлах; граничные условия - варьируемые входные данные (величины притоков и нагрузок, допустимые диапазоны гидравлических параметров). Поскольку каждому узлу и каждой ветви гидравлической цепи составляется узел и ветвь графа, граф цепи содержит всю информацию о соединениях и геометрических свойствах исходной цепи. На рис.1,а,б соответственные узлы, а также ветви цепи и графа имеют одинаковые номера.

Граф, также как и исходная цепь, может иметь различную структуру. Различают планарный (плоский) граф, если его можно изобразить на плоскости без пересечения ветвей (рис.1,б) и непланарный (пространственный) граф, если при его изображении на плоском чертеже невозможно избежать пересечения ветвей (рис.3,а).

Любую часть графа, элементы которой являются элементами исходного графа, называются подграфом, подграф получают путем удаления (исключения) некоторых ветвей исходного графа.

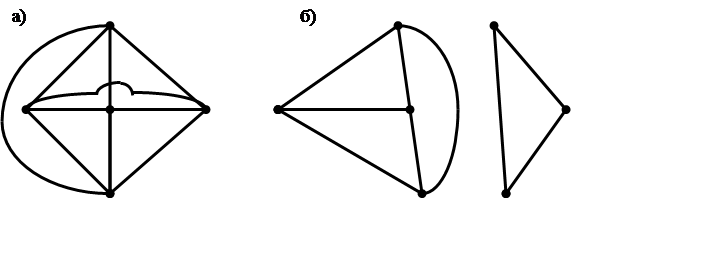Рис.3. Примеры графов:

 а - непланарный граф; б - несвязный граф

Важным подграфом является путь графа, представляющий непрерывную                последовательность ветвей, каждая из которых связывает пару выбранных узлов, с прохождением каждого узла не более одного раза. Смежные ветви пути имеют общий узел, так что к каждому узлу присоединены две ветви, лишь к крайним узлам по одной ветви.

Если в заданном графе имеется хотя бы один путь между любой парой узлов, то граф называется связным - он соответствует цепи, элементы которой соединены гидравлически (рис.1,б и 3,а). Граф (рис.3,б) является примером несвязного графа: он состоит из двух раздельных частей, элементы которых могут иметь связь, например, через теплообмен.

Для составления уравнений соединений по сетевым законам Кирхгофа на ветвях графа цепи указывают стрелками положительные направления движения жидкости. Использование ориентированного графа цепи позволяет производить аналитическую запись структуры графа и подграфов в виде матриц, называемых топологическими матрицами. Аналитическое представление графа необходимо для формирования уравнений сложной цепи с помощью ЭВМ.