Основы гидравлического расчета трубопроводных систем на ЭВМ: Методические указания к практическим занятиям по курсам “Проектирование, монтаж и испытание судовых систем” и “Производство и распределение энергоносителей промышленных предприятий”, страница 6

Контур представляет собой замкнутый путь, у которого только начальный и конечный узлы. При этом к каждому узлу оказываются присоединенными по две ветви, входящие в контур. Следовательно, контуром графа называется связный подграф, к каждому узлу которого присоединены только по две ветви. На рис.4,б замкнутыми пунктирными линиями показаны несколько контуров графа. Перечислим ветви, входящие в некоторые контуры: a - I, 2, 4; b - 2, 6, 3;  g - 2, 5, 6 и т.д. Очевидно, контурами являются все внутренние ячейки плоского графа (a,b), которые можно определить как контуры, не охватывающие ни одной ветви. Легко убедиться в том, что число возможных контуров графа может быть намного больше числа ячеек.

Рис.4. Сечения и контуры графа

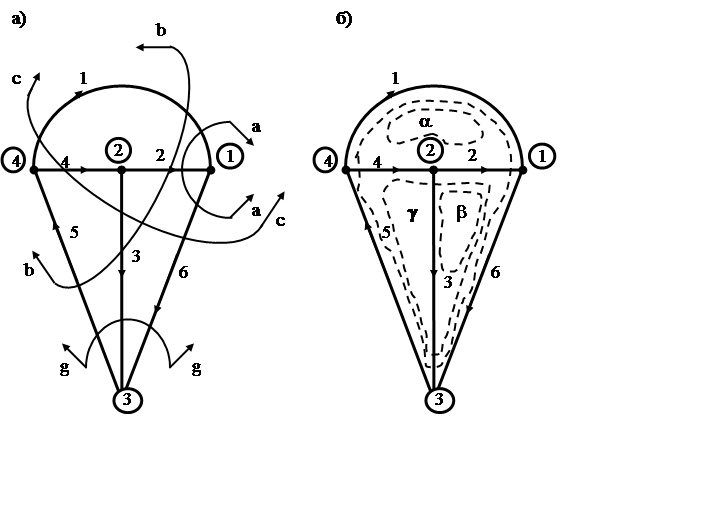
Уравнения второго закона Кирхгофа составляются для контуров графа цепи, а первого закона Кирхгофа могут составляться для сечений графа. Последнее положение следует из обобщенной формулировки первого закона Кирхгофа: алгебраическая сумма расходов ветвей сечения равна нулю. Обобщение первого закона Кирхгофа является простым следствием обычной его формулировки расходов ветвей в узлах.

Не приводя доказательства, отметим следующее важное положение: общее число уравнений, составленных для множества сечений и контуров заданного графа, может быть намного больше необходимого числа уравнений. Это означает, что уравнения будут зависимыми - часть из них будет следствием остальных, т.е. лишней. Из множества сечений и контуров графа цепи необходимо выбрать такие, которые дают линейно-независимые системы уравнений, составленные по законам Кирхгофа. Сечения и контуры, дающие линейно независимую систему уравнений, называемые главными сечениями и главными контурами, удобно вводить с помощью понятия дерева графа.

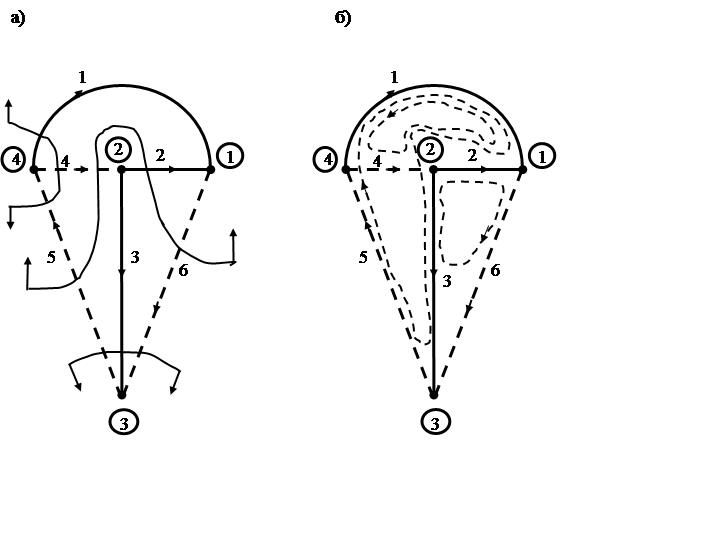
Деревом называют подсхему без контуров, соединяющую все узлы и имеющую    (m – 1) ветвей. Дерево, соответствующее этому определёнию называют в теории графов остовом графа или остовным деревом. Остовное дерево получается путем удаления ветвей, образующих контуры. Между любой парой узлов дерева имеется единственный путь. На рис.5,а приведено одно остовное дерево графа (см.рис.1,б). Число возможных остовных деревьев графа очень быстро растет с усложнением его структуры.

Рис.5. Главные сечения и контуры графа

Для полного графа число возможных остовных деревьев равно m^m-1. Ниже остовное дерево будем называть просто деревом.

Построение дерева разбивает ветви графа на ветви дерева и ветви, не вошедшие в него, которые называют хордами. На рис.5,а ветви дерева нанесены сплошными линиями, а хорды пунктирными. Число ветвей дерева на единицу меньше числа узлов. Это следует из того, что первая ветвь соединяет два узда, а каждая последующая присоединяет один узел, так что число ветвей дерева будет:

Число хорд, т.е. ветвей не вошедших в дерево:

Для получения главных сечений главных контуров связного графа выбирают определенное дерево. Каждой ветви дерева можно сопоставить единственное главное сечение, которое состоит из одной ветви дерева и нескольких хорд. Каждое главное сечение включает в себя только одну ветвь дерева, которая не входит в другие сечения. Поэтому уравнение первого закона Кирхгофа в главных сечениях будут независимыми. Число главных сечений равно числу ветвей дерева n_д. На рис.5,а показаны все три главных сечения графа. Принята следующая нумерация ветвей: первые номера получают ветви дерева, остальные номера получают хорды. Главным сечениям приписаны номера ветвей дерева, входящих в эти сечения. Такая нумерация приводит к удобному упорядоченному виду матриц. Может быть и другая нумерация, также приводящая  к упорядоченному виду матриц, когда первые номера присваивают хордам, а остальные ветвям дерева.

Матрица главных сечений Q описывающая соединения ветвей, входящих в независимые сечения, представляет таблицу, n_д строк которой является порядковыми номерами сечений, совпадающими с номерами ветвей дерева, и nстолбцов - номерами всех ветвей. Элементы матрицы равны +1 при совпадении, -1 при несовпадении направления ветви с выбранным положительным направлением сечения (по направлению расхода в ветви дерева) и 0, если ветвь не входит в сечение.