Для формирования матриц Q и B матрицу A также формируют в упорядоченном виде. Матрицу (11) в соответствии с принятой нумерацией ветвей можно также «расщепить» на матрицы дерева Ад и хорд Ах:
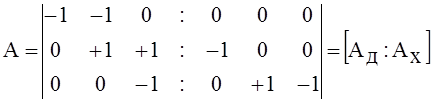
Как уже отмечалось выше, может быть принят и иной порядок нумерации ветвей, чем на рис.5: первые номера присваиваются хордам, а последующие - ветвям дерева. В этом случае матрицы цепи примут вид:
; 
; 
, а нумерация контуров
принимает более естественный вид:
с = (1,…,nx).
6. Математические модели потокораспределения
Математическое моделирование всегда является приближенным и его точность в основном определяется выбором модели гидравлической цепи одного из следующих типов:
1) С сосредоточенными параметрами, когда все технические параметры узлов и ветвей, а также граничные условия являются константами, не зависящими от потокораспределения.
2) С переменными параметрами, когда хотя бы часть технических параметров является функцией потокораспределения.
3) С распределенными параметрами в случае наиболее строгого описания совместного изменения гидравлических параметров вдоль элементов расчетной схемы.
С математической точки зрения это приводит к системам уравнений следующих структур:
- из линейных (сетевых) и нелинейных замыкающих алгебраических уравнений с постоянными коэффициентами;
- из уравнений общего характера с переменными коэффициентами и правыми частями;
- смешанных систем, содержащих подсистемы уравнений в дифференциальной и интегральной форме;
Для расчета гидравлических цепей используются методы контурных расходов (МКР) и узловых давлений (МД). Оба метода (особенности применения, алгоритмы, вопросы точности и пр.) достаточно подробно освещены в научной литературе. Метод контурных расходов - аналог известного метода контурных токов для расчета линейных электрических цепей, а метод узловых давлений - метода узловых напряжений, которые достаточно подробно изложены в учебной литературе. По теории электрических цепей. Ниже приводятся основные системы уравнений, описывающие потокораспределение в произвольной гидравлической цепи с сосредоточенными параметрами и являющимися исходными для МКР и МД.
Если по знаку величины Vi необходимо судить о направлении потока на участке (ветви) и соответственно о знаке DРi, то уравнение (7) можно записать в виде:
(19)
где Рнi= 0 в случае пассивной ветви, т.е. не содержащей нагнетателя.
Путем введения диагональных матриц:
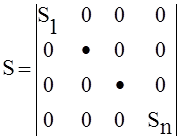и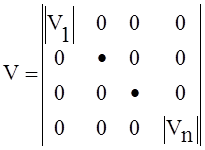 
, а также векторных обозначений 
, DР , Рн
соотношения (19) можно записать в компактной форме сразу для всей схемы :
(20)
В методе контурных расходов в качестве переменных принимают расходы. Математическая модель этого метода сводится к системе уравнений:
;
;
(21)
.
Уравнения (20), составляющие здесь последнюю группу из n уравнений называются замыкающими соотношениями. Они дополняют уравнения первого закона (13) и nx уравнений второго закона (18) Кирхгофа до полной системы (21) из 2n уравнений относительно неизвестных Vi и DPi.
В системе (21) можно исключить вектор DP путем подстановки (20) в (18):
(22)
и тем самым её порядок понижается от 2n до n , при этом неизвестными являются расходы Vi. Система (22) является исходной в МКР. Метод контурных расходов применим для гидравлических сетей, приведенных к графу транспортной сети или для циркуляционных схем.
В методе узловых давлений математическая модель опирается на использование в качестве независимых переменных, помимо расходов Vi, узловых давлений Рj (j=1,…, m-1) относительно узлового давления Pm узла m, выбранного в качестве опорного или базисного. Независимые узловые давления Рj (j=1,…, m-1) вместе с заданным давлением Pm составляют вектор Р. Соответствующая ей система уравнений не требует обращения к контурам, так как при любом векторе Р уравнения второго закона Кирхгофа обращаются в тождество. Вместо этого вводится связь между потерями напора DРi и давлениями в узлах Pi, имеющая для ветви i=[j,j+1] вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.