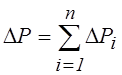, а
приведенное сопротивление сети при V1=Vi ( i=1,2,… ,n) равно сумме приведенных сопротивлений отдельных её
элементов:
.
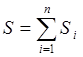При параллельном соединении элементов участков сети потери давления в каждом из них равны между собой DР1=DРi ( i=1,2,… ,n),а расход в сети
.
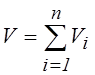Отсюда следует, что суммарная проводимость параллельно соединенных элементов равна сумме проводимостей этих элементов
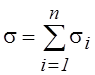, а с учетом уравнения (6) приведенное сопротивление:
.
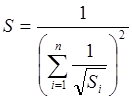Расход через каждый элемент (при параллельном соединении) при известных проводимостях:
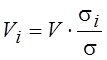
или при известных приведенных сопротивлениях:
.
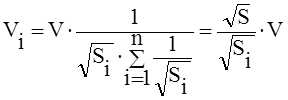Для участков сети, на которых находятся нагнетатели уравнение (3) будет иметь вид:
,
(7)
где Рнi - активный напор нагнетателя, Па. При постоянной частоте вращения рабочего колеса рабочий участок характеристики центробежного насоса может быть приближенно описан уравнением:
,
(8)
где Р0i - напор насоса при расходе Vi=0; S0i - условное внутреннее приведенное сопротивление насоса, Па×с2/м6.
В случае нагнетателей других типов аналитические напорные характеристики могут иметь иной вид, чем уравнение (8).
Приведенные выше уравнения метода по приведенным сопротивлениям могут быть в полном объеме использованы при гидравлическом расчете малоразветвленных сетей с помощью упрощенных вычислительных методов. В случае решения полной системы уравнений гидравлического расчета сети с помощью численных итерационных методов используются выше приведенные уравнения (3…8).
4. Сетевые законы Кирхгофа
Два фундаментальных сетевых закона Кирхгофа играют центральную роль в теории гидравлических цепей, которые можно сформулировать следующим образом:
Первый закон Кирхгофа: алгебраическая сумма расходов в любом узле j равна нулю:
, где:
åVi – алгебраическая сумма расходов по всем участкам i,
имеющим общий узел j; Uj – расход в
узле: нагрузка Uj > 0, если
в узле j находиться потребитель, приток Uj < 0, если
в узле j находиться источник, и Uj =
0, если узел j
является простой точкой разветвления потоков в схеме.
Второй закон Кирхгофа: алгебраическая сумма потерь напора для любого замкнутого контура равна нулю.
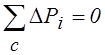, где
с – номер контура.
Уравнения, составленные по законам Кирхгофа, носят алгебраический характер и зависят только от взаимосвязи элементов в цепи, а не от их природы.
5. Граф и гидравлическая цепь
Применение понятия графа позволяет записывать в матричной форме уравнения соединений, составляемые на основе законов Кирхгофа, и тем самым формировать уравнения гидравлической цепи с помощью ЭВМ. Поэтому при составлении уравнений удобно отвлекаться от вида и характеристик элементов гидравлической цепи, заменив их линиями. Например, для гидравлической цепи, показанной на рис.1,а получим граф, показанный на рис.1,б.
Дадим понятию графа математическое определение. Граф является системой или совокупностью двух множеств – вершин j , изображаемых точками и ребер i, изображаемых отрезками линий, которые соединяют пары вершин (на рис.1,б номера вершин j указанные в кружках, а рядом с каждым ребром i - его номер без кружка). Если ребро графа определяется парами вершин, то говорят, что ребро инцидентно этим вершинам. В том случае, если ребра графа определяются упорядоченными парами вершин (начальными и конечными), то ребра часто называют дугами. На каждой дуге ставят стрелку, указывающую её ориентацию от начальной вершины к конечной. В результате получается граф с ориентированными ребрами (дугами), называемый ориентированным графом. Дуга называется исходящей из своей начальной вершины и заходящей в свою конечную вершину. Степенью d(j) вершины j называется число инцидентных ей дуг. Полустепенью захода d-(j) вершины j является число заходящих дуг в вершину j, а полустепенью исхода d+(j) - число исходящих из вершины j дуг.
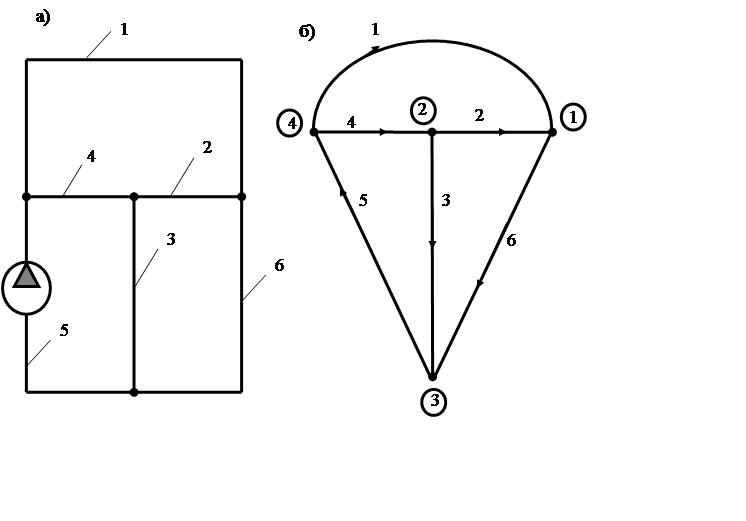
а – гидравлическая цепь; б – ориентированный граф.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.