Основы гидравлического расчета трубопроводных систем на ЭВМ: Методические указания к практическим занятиям по курсам “Проектирование, монтаж и испытание судовых систем” и “Производство и распределение энергоносителей промышленных предприятий”, страница 10

В методе контурных расходов (МКР) процесс последовательных приближений (итераций) для расходов:

                                          (28)

осуществляется таким образом, что для любого  выполняются условия (22) первого закона Кирхгофа в узлах. Для этого достаточно, чтобы этим условиям удовлетворяло начальное приближение:

, а все приращения (поправки)  к расходам имели бы нулевые балансы:

.                                  (29)

Из (28) следует, что в качестве независимых (свободных) переменных можно взять приращения к расходам на хордах  тогда соответствующие им поправки к расходам на ветвях дерева  будут определяться следующим образом:

.                                        (30)

При этом здесь не надо обращать матрицу А_д, поскольку из (15) и (17) следует:

.                                    (31)

Отсюда получим:

.                     (32)

Что касается  , то эти приращения к расходам на хордах выбираются из условия уменьшения невязок, которые получаются при подстановке в (22) очередного приближения :

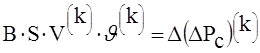                                  (33)

где D(DР_с)^(k) - вектор-столбец невязок напоров, вычисленных для контуров по данным k-ой итерации. Для пассивных контуров:

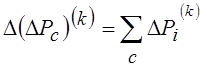, а для контуров, содержащих активные ветви с источниками напора

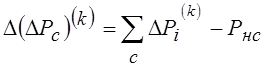, где 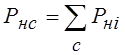 является алгебраической суммой активных напоров, действующих на ветвях, входящих в контур.

Целью является добиться выполнения равенства:

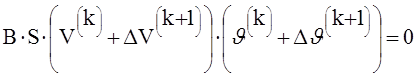
Раскрывая здесь скобки, пренебрегая членами, содержащими  и подставляя вместо  его выражение (32) через , придем с учетом (33) к системе линейных уравнений:

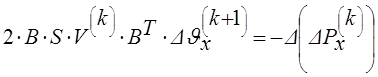,                             (34)

которую надо решать на каждом шаге вычислительного процесса.

Симметричная матрица этой системы:

имеет смысл матрицы Максвелла, впервые рассмотревшего преобразование переменных к контурным величинам.

Путем обращения матрицы М^(k) или непосредственного решения системы (33) каким-либо из методов линейной алгебры определяются приращения расходов на хордах ,а по ним (по формулам (30) и (31) вычисляются поправки  к расходам на ветвях дерева. Это позволяет получить новое приближение (28) для вектора расходов. Далее проводится анализ сходимости вычислительного процесса:

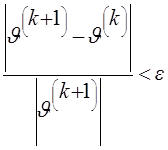
По новому приближению  опять формируется и решается система уравнений (34) и т.д.

Преобразования Максвелла особенно эффективны в том случае, если остовное дерево цепи выбрано таким образом, что соответствующая ему система главных контуров представляет собой элементарные ячейки, причем ни одна из ветвей не принадлежим более  чем двум контурам, т.е. схема оказывается плоской. Признаком плоской схемы является наличие в каждом столбце матрицы В не более двух не нулевых элементов +1 или -1, т.е. каждая ветвь входит не более чем в два контура.

От выбора начального приближения во многом зависит, как отмечалось выше, сходимость метода Ньютона-Рафсона. Начальное приближение для расходов  можно определить путем решения одним из стандартных методов линейной алгебры линеаризованной системы уравнений, получающейся из исходной нелинейной системы (22). Линеаризованная система уравнений будет иметь вид:

  ;   , где

  ; .

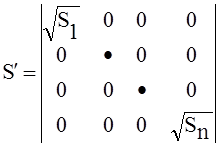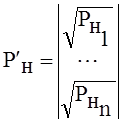Основной алгоритм МКР сводится к выполнению следующих операций:

1)  Схема приводится к графу транспортной сети (см. например, рис.2) или к циклической схеме с помощью дополнительных фиктивных ветвей, не имеющих сопротивления . Для схем, обладающих естественной цикличностью (циркуляционные системы) выполнение этой операции не требуется.

2)  Подготавливаются исходные данные для ввода в ЭВМ. На схеме выделяется некоторое дерево, связывающее все ее m узлов. В результате все ветви разобьются на m – 1 ветвей дерева и n_x ветвей, не вошедших в дерево, называемых хордами, при этом в качестве корня дерева удобно задавать источник (нагнетатель). Намечаются произвольные направления потоков в ветвях схемы и подготавливаются редуцированная матрица соединений  А и матрица главных контуров В. Каждая хорда замыкает какую-то последовательность участков дерева и однозначно определяет контур, который и фиксируется соответствующей строкой в матрице В.