Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 9

среднего значения   в тот же момент времени;

величины δq_j (изменения q в частице на пути от точки поворота до площадки);

величины (отклонения q_j от среднего для уровня поворота z_j в момент t_j);

изменения среднего значения q на пути от точки z_j,t_j к точке z,t.

Подставляем полученное соотношение в выражение для плотности турбулентного потока:

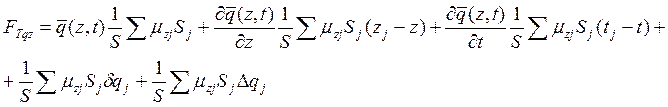
Проанализируем отдельные члены. Первый член равен нулю, так как    , а мы договорились, что адвективный поток вдоль z отсутствует.

Третий член пропорционален   , причем всегда (t_j-t)<0, поскольку t_j < t.  Частицы, приходящие к площадке сверху, дают положительный вклад в сумму, частицы снизу - отрицательный. Эти вклады приблизительно равны по величине, поэтому данным членом можно пренебречь.

Второй член. Здесь мы учтем, что относительные колебания плотности частиц малы, и можно приближенно положить[12]  ρ_j≈ρ.  

Тогда                                                                        

                               ,

причем все слагаемые в правой части больше нуля. Обозначим

                                                                                                        (15.10)

и назовем коэффициентом турбулентного перемешивания или турбулентной диффузии. Как видно, в него входят скорости частиц воздуха, пересекающих в данный момент нашу площадку, и расстояние от площадки до точки поворота этих частиц[13].

Коэффициент никак не связан со спецификой физической величины q, он характеризует только кинематические свойства турбулентного движения. Поэтому вертикальные турбулентные потоки самых различных физических величин выражаются через тот же самый коэффициент   k_z.  Следует, однако, помнить, что его величина зависит от особенностей турбулентного движения: чем больше удаление точки поворота воздушной частицы и чем выше скорость (вернее импульс) при пересечении площадки – тем больше величина коэффициента.

Обратимся теперь к оставшимся двум членам. Опять пренебрежем колебаниями плотности воздуха в различных частицах (отклонения  ρ_j от среднего значения ρ, как легко убедиться, дают квадратичный вклад по флуктуациям  δρ_j ∆q_j или δρ_j δq_j). Тогда эти два члена можно представить в виде

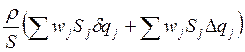                                      .                                                           (15.11)

Можно сказать, что эти две суммы до некоторой  степени отражают влияние вертикальных движений на изменение величины q в частицах и обратное влияние изменений в q на вертикальные перемещения.

Действительно, δq_j  - есть изменение q в процессе движения от точки поворота до площадки.  Если для групп частиц, движущихся с одинаковыми скоростями вверх и вниз, суммы величин    S_jδq_j  окажутся одинаковыми, то первый член обратится в ноль.  Но это значит, что изменение q в процессе движения частиц непосредственно не связано с характером этого движения (в данном случае с направлением движения).                                                                                                  

Во втором члене   есть отклонение значения q в j-й частице от среднего значения величины   в точке поворота.  Если для групп частиц, движущихся с одинаковыми скоростями вверх и вниз, суммы величин S_j окажутся равными, то второй член обратится в ноль. Это можно интерпретировать, как то, что конкретные значения величины q в частицах не влияют на характер их движения (в данном случае на направление движения).

На самом деле условия обращения в нуль обеих рассмотренных сумм являются менее жесткими, чем условия Келлера (консервативности и пассивности). Оказывается, что они с хорошей точностью соблюдаются для многих физических величин (удельная влажность, концентрация ионов, запыленность воздуха, концентрация ядер конденсации и т.д.). Приближенное выражение для вертикального турбулентного потока всех этих величин

                                                . 

Однако для турбулентного потока тепла (плотности потока теплосодержания воздуха - с_рТ) ни один из рассмотренных членов в нуль не обращается.