Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 10

Прежде чем переходить к рассмотрению проблемы переноса тепла, исследуем другой частный случай. Пусть физической величиной является составляющая скорости в направлении оси x: q=u. Тогда, согласно определению, вертикальная составляющая вектора плотности потока импульса, обусловленная турбулентным характером движения в условиях адвекции в направлении горизонтальной оси x,

                              .

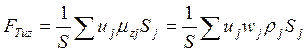Мы по-прежнему рассматриваем ситуацию, когда адвективное движение в направлении оси z отсутствует. Это значит, что  , то есть, . Поэтому

       ,

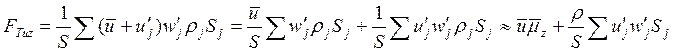где мы опять пренебрегли изменением плотности. Последняя сумма в приведенном выражении есть ни что иное, как  согласно избранной процедуре усреднения. Поэтому, используя ранее введенные обозначения, получаем

                                                          ,

где ρT_xz – компонента тензора турбулентных напряжений. Таким образом, плотность турбулентного потока импульса непосредственно связана с тензором турбулентных напряжений, введенным нами при рассмотрении процедуры осреднения уравнений движения. Просто здесь конкретизирована процедура осреднения, и она не противоречит выводам, полученным ранее.  Тогда же была предложена аппроксимация

                                       ,

которая оказывается правомочной, если для избранной физической величины выражение (15.11) близко к нулю. Простые рассуждения, на первый взгляд, показывают, что ни изменение горизонтальной составляющей скорости на пути от точки поворота к площадке, ни флуктуации горизонтальной составляющей скорости в точках поворота не могут привести к возникновению некомпенсированных вкладов в (15.11); следовательно предложенная аппроксимация вполне обоснованна[14].

Замечание. В отличие от молекулярной вязкости, где коэффициент кинематической вязкости ν – характеристика микроскопических свойств жидкости или газа, коэффициент турбулентной вязкости является характеристикой кинематических свойств среды в данной точке пространства, то есть, зависит от характера движения жидкости и является функцией координат (а, может, и времени, если свойства движения в данной точке пространства меняются во времени). Это значит, что коэффициент турбулентной вязкости  не есть свойство среды, а есть, в первую очередь, характеристика движения среды. В зависимости от того, как движется среда, получаются разные коэффициенты, причем, разные в разных направлениях. Мало того, что введение коэффициента турбулентной вязкости есть аппроксимация реальности. Оказывается, что для расчета хотя бы приближенного движения среды (усредненного) нужно знать эти коэффициенты во всех точках пространства. А чтобы получить эти коэффициенты, нужно знать движение среды. Получается замкнутый круг, который разрывается посредством использования моделей,  гипотез и экспериментальных данных для определения  коэффициентов турбулентной вязкости.

15.3. Турбулентный поток тепла

Вертикальный турбулентный поток тепла

Здесь мы опять рассматриваем вертикальное направление в условиях упорядоченного горизонтального движения. Согласно проведенному в предыдущем разделе анализу, для плотности вертикального турбулентного потока тепла имеем

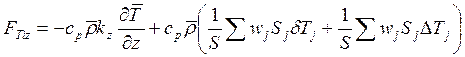       .                                  (15.12)

Изменение температуры движущейся частицы воздуха (в условиях отсутствия фазовых превращений воды) вызывается двумя причинами:

1.  непосредственным притоком тепла со стороны или, наоборот, отдачей тепла окружающей среде;

2.  увеличением внутренней энергии частицы при сжатии и уменьшением при расширении.

Тепловое взаимодействие частицы со средой не связано с ее движением и происходит весьма медленно. Поэтому в пределах достаточно коротких временных интервалов первую причину можно игнорировать.

Что касается другой причины изменения температуры, то мы будем считать, что вертикальные перемещения частицы происходят без теплообмена с окружающей средой. Это полностью согласуется с первым предположением и означает, что сжатие и расширение частицы происходят адиабатически. Тогда