Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 2

Турбулентное движение так же осуществляет перенос различных физических характеристик воздуха, как это имеет место в случае ламинарного (упорядоченного) движения, однако в случае турбулентного движения этот перенос происходит намного эффективнее.

«Механизм» перехода от ламинарного течения к турбулентному

Весьма оригинальные результаты, касающиеся перехода от ламинарного движения к турбулентному, получены  Л.Д. Ландау [36]. Исходной посылкой его анализа является то, что для любой задачи о движении вязкой жидкости в заданных стационарных условиях должно существовать точное стационарное решение уравнений гидродинамики. Формально такие решения должны существовать при любых числах Рейнольдса. Однако не всякое стационарное  решение, даже если оно является точным, может реализоваться в природе. Реально осуществляющиеся стационарные движения должны не только удовлетворять уравнениям движения, но также и быть  устойчивыми по отношению к малым возмущениям. То есть, возникающие малые возмущения движения должны затухать со временем. В противном случае движение оказывается неустойчивым и реально существовать не может.

Идея анализа устойчивости стационарного решения  по отношению к малым возмущениям оказывается весьма плодотворной для понимания процесса перехода от ламинарного движения к турбулентному. В дальнейшем такое понимание может быть распространено и на движения в нестационарных условиях.

Анализ устойчивости движения сводится к наложению на стационарное решение с распределением скоростей  малого возмущения , которое определяется так, чтобы результирующее движение  также удовлетворяло уравнениям движения. Подставляя результирующее выражение для скорости в уравнения движения для несжимаемой жидкости и отбрасывая члены высших порядков малости, находим

           ,

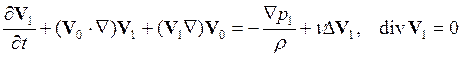где введено обозначение  и учтено, что известные функции  также удовлетворяют уравнениям движения. Граничным условием является обращение вклада в скорость за счет возмущения в ноль на неподвижных поверхностях. Из приведенного уравнения следует, что  удовлетворяет системе однородных линейных дифференциальных уравнений с коэффициентами, являющимися функциями только координат, но не времени. Общее решение подобных систем может быть представлено суммой частных решений, в которых  зависит от времени по закону . При этом частоты возмущений ω определяются на основании требования выполнения граничных условий. В общем случае эти частоты будут комплексными величинами. Если обнаружатся частоты с положительной мнимой частью, функция  будет неограниченно возрастать со временем. Иными словами, соответствующие возмущения будут усиливаться, и начальное движение будет неустойчивым. Такая неустойчивость в конечном счете и приводит к возникновению турбулентности.

Опыт показывает, что при достаточно малых числах Рейнольдса стационарное движение получается устойчивым. По мере увеличения числа Рейнольдса достигается некоторое его критическое значение Re_кр, начиная с которого движение становится неустойчивым. Конечно, для каждого движения это критическое значение индивидуально. Рассмотрим свойства движения при  значениях Re, не намного превышающих критическое значение. Очевидно, при Re<Re_кр у комплексных частот всех возможных возмущений мнимая часть отрицательна, поскольку стационарное движение устойчиво. При Re=Re_кр  появляется хотя бы одна частота, мнимая часть которой обращается в ноль. При Re>Re_кр  у этой частоты  мнимая часть становится положительной, причем естественно ожидать, что для чисел Рейнольдса, близких к критическому значению,  величина мнимой части будет много меньше вещественной части частоты возмущения.