Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 8

1.Величина q обладает свойством консервативности, то есть, значение q в каждой воздушной частице сохраняется при движении, а при смешении двух частиц общее количество величины q получается путем сложения индивидуальных значений.

2. Величина q обладает свойством пассивности, то есть, конкретное значение q в частице не влияет на ее движение.

Следует сразу заметить, что перенос наиболее важных величин, например,  таких, как  теплосодержание, не удовлетворяет условиям Келлера.  Поэтому актуальное значение приобретает выяснение вопроса: какие изменения должны быть внесены в формулу в случае нарушения свойств консервативности и пассивности? Во-вторых, полезно узнать смысл коэффициента вертикального перемешивания k_z , каковы его значения в различных условиях, и то же самое - для коэффициентов перемешивания в горизонтальном направлении.

Поэтому мы продолжим исследование выражения для F_T . Напомню, предполагается, что адвективный поток вдоль z отсутствует, и для турбулентной составляющей плотности потока справедливо выражение (15.3):

                                         .

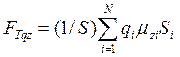Следует также напомнить, что адвективный поток определен в соответствии с житейским пониманием среднего:

                      ,

хотя используемая процедура осреднения весьма оригинальна (оперирует сечением частиц, пересекающих площадку) и отличается от более привычного усреднения по времени или по объему. Оказывается, что для нашего анализа такая процедура предпочтительнее.

Теперь, чтобы двигаться дальше, нам нужно учесть какие-то принципиально важные характеристики турбулентного  движения. Для этого нет необходимости глубоко вдаваться в теорию, тем более, что самые совершенные теории турбулентности носят в сильной степени модельный характер[11], поскольку строгое механическое рассмотрение хаотического турбулентного движения на практике невозможно.

Так, в качестве важнейшей характерной особенности турбулентного движения мы используем то, что частицы, пересекающие площадку, совершают вихревое движение. Поэтому в подавляющем большинстве случаев можно утверждать, что частицы воздуха, пересекающие уровень z в момент времени t, в некий предыдущий момент t_j < t (свой для каждой частицы) имели нулевую составляющую вертикальной скорости на некоторой высоте z_j: w_j (z_j,t_j) = 0  (в точке поворота в момент поворота, см. рис. 15.2).   При этом выполняются очевидные неравенства                       

                                   если ,

                                    если ,

(здесь рассматривается момент времени пересечения площадки, более поздний, чем момент поворота).

Оказывается, что если мы явно учтем данное обстоятельство, этого будет достаточно, чтобы охарактеризовать турбулентное движение с нужной полнотой.

Давайте сначала представим значение q_j(z_j,t_j) в виде             

                                            ,                                                           (15.7)

где ∆q_j – отклонение от среднего значения величины q в частице с номером j в момент времени t_j на уровне z_j.  Затем введем разность

                                                                                                         (15.8)

- изменение величины q в момент времени t пересечения площадки на уровне z по сравнению с тем, какой она была, когда вертикальная скорость частицы j равнялась нулю (то есть, изменение физической величины в частице за время движения от точки поворота к площадке). Тогда можно записать                                                                   

                        .                                            (15.9)

Теперь уместно разложить  в ряд Тейлора по степеням (z_j-z) и (t_j-t) около точки z,t. При этом будем считать, что обе разности малы, и членами выше первого порядка можно пренебречь (это разумно, поскольку мы ожидаем вполне гладкой зависимости средних значений от координат и времени).                                     

               .

Таким образом, мы определили значение q  j-й частицы на уровне z в момент времени t в виде суммы