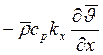 ,
,
которое
отличается от плотности потока обычного тепла тем же множителем ![]() .
.
Выражение, аналогичное (15.15), справедливо для плотности потока в направлении оси y. Как видите, горизонтальный турбулентный поток тепла отсутствует в тех случаях, когда отсутствует горизонтальная составляющая градиента потенциальной температуры.
Турбулентность и масштаб осреднения
Чем больше детализируется среднее движение (чем меньше масштаб осреднения), тем значительнее роль адвективного и слабее роль турбулентного потока, хотя сумма остается прежней. Отсюда следует, что для различных масштабов и коэффициент турбулентной вязкости будет иметь разные значения (в частности, он стремится к коэффициенту молекулярной вязкости, если устремить масштаб осреднения к нулю и перейти к неосредненным уравнениям динамики атмосферы).
Формальный аппарат теории турбулентного обмена с успехом был применен для описания суммарного переноса тепла циклонами и антициклонами в общей циркуляции атмосферы. При этом пришлось использовать очень большие (порядка 106 м2/с) значения коэффициента «макротурбулентного перемешивания».
Во избежание ошибок в интерпретации результатов расчетов следует постоянно помнить о масштабе осреднения. Посредством введения коэффициента турбулентной вязкости мы несколько упрощаем уравнения движения, и в некоторых случаях появляется возможность их аналитического решения (см. разд. 16.2). Однако попытка интерпретировать детали такого решения, меньшие по размеру масштаба осреднения, очевидно, будет некорректной. Действительно, выбор значения коэффициента турбулентной вязкости в соответствии с заданным масштабом осреднения как раз и призван ликвидировать мелкомасштабные детали движения при сохранении крупномасштабных.
[1] Ввиду осевой симметрии задачи.
[2] Осборн Рейнольдс (Reynolds, 1842-1912) английский физик.
[3] Представление о турбулентных движениях воздуха проще всего получить, наблюдая за струйкой дыма от сигареты.
[4] Над морем нижний ламинарный слой имеет толщину в несколько миллиметров. Над сушей ламинарный слой прерывается вблизи неровностей и шероховатостей.
[5] Уравнения движения жидкости или газа по сути есть результат осреднения движения составляющих их атомов и молекул, приводящего к концепции «сплошной среды», и уже по этой причине являются приближенными. Процедуру дальнейшего осреднения в некотором смысле можно интерпретировать, как переход от рассмотрения среды как совокупности самых мелких структурных элементов (атомов и молекул, тепловое движение которых является источником обычной вязкости газа или жидкости) к рассмотрению более крупных структурных образований типа воздушных частиц, воздушных масс и т.д. Очевидно, что в этом случае нужно будет переопределить определение вязкости уже на языке нового структурного состава среды, как процесс «диффузии» новых структурных элементов. В отличие от «примитивного» теплового движения атомов и молекул, здесь оказывается, что поведение более крупных образований зависит от особенностей осредненного движения. К тому же возможность нестационарных решений уравнений движения при стационарных граничных условиях не исключается полностью: осредненные уравнения движения остаются нелинейными и по виду совпадают с исходными. Просто условия перехода от «ламинарного» осредненного движения к «турбулентному» начинают зависеть от масштаба осреднения.
[6] И, вообще говоря, такая связь почти всегда есть.
[7] Соотношение справедливо, если выполняется условие . Тогда вклад от такого члена равен нулю, поскольку по определению . Однако приведенное условие выполняется только в случае, когда среднее значение не зависит от параметра, по которому проводится осреднение (например, от времени, если исследуется среднее по интервалу времени значение скорости). Мы в дальнейшем предполагаем, что так и есть на самом деле. Однако такое предположение в каждом конкретном случае требует строгого обоснования [17].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.