Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 6

При решении подобного рода задач мы сталкиваемся с понятием потока физической величины – количеством физической величины, переносимой через заданную поверхность за единицу времени. Мы уже знакомились  с этим понятием на примере потока излучения при изучении переноса излучения в атмосфере. Здесь, правда, имеется существенная разница. Поток излучения  определялся как количество электромагнитной энергии, переносимой через единичную площадку со всех направлений за единицу времени. Подразумевалось, что электромагнитное излучение может поступать в заданную точку пространства по произвольному направлению. Это предположение неверно, когда речь идет о  переносе физических величин, связанных со средой. В этом случае физические величины являются характеристиками частиц среды и, очевидно, переносятся вместе с движением самой среды.  А движение происходит в направлении вектора скорости. Больше не существует других направлений, откуда мог бы осуществляться перенос физических величин, связанных со средой. Поэтому можно ввести понятие  вектора плотности потока физической величины, определяющего количество физической величины, переносимой за единицу времени через перпендикулярную направлению ее переноса единичную площадку, и совпадающего по направлению с вектором скорости переноса физической величины.. Нечто подобное подразумевалось, когда речь шла о параллельном пучке излучения, например, от Солнца.  Для потока произвольной физической величины q через заданную поверхность (не обязательно плоскость) S справедливо выражение

                                            ,

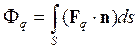где -  вектор плотности потока физической величины, n– вектор нормали к элементу ds поверхности, интегрирование ведется по всей рассматриваемой поверхности. Нас, в первую очередь, будет интересовать плотность потока тепла.

Перенос тепла вместе с движущимися воздушными частицами называется конвекцией[9]. За единицу времени через единичную площадку перпендикулярно направлению скорости проходит масса воздуха ρV (здесь V – величина скорости!), теплосодержание единицы массы i = c_рТ. Поэтому для плотности конвективного потока тепла получаем

F_К=c_рТρV                                                                                 (15.1)

- вектор плотности конвективного потока тепла (количество тепла, переносимого воздухом за единицу времени через единичную площадку, перпендикулярную направлению скорости). ЗдесьV – вектор скорости воздуха. Плотность конвективного потока тепла F_К   можно разделить на 2 составляющие: плотность потока F_А, обусловленного упорядоченным перемещением частиц воздуха с некоторой средней скоростью V_A и потока  F_Т , обусловленного неупорядоченными турбулентными движениями со скоростьюV_Т, согласно принятой схеме разделения скорости  на две составляющие:

                                       V=  V_А + V_Т        →               F_К = F_А + F_Т  .

Такое разделение, очевидно, носит субъективный характер, поскольку зависит от масштаба и от способа осреднения. Чем меньше этот масштаб, тем бόльшая часть потока физической величины обусловлена «упорядоченным» переносом. Обратите внимание, что векторы F_А  и F_Т обладают разными свойствами. Во-первых, F_А - вектор, плавно меняющий свою величину и направление по сравнению с быстро флуктуирующим вектором F_Т . Во-вторых, последующее осреднение вектора F_А в рамках процедуры, использованной для определения составляющей средней скорости V_А, не меняет его. Однако осреднение быстро флуктуирующего вектора F_Т приводит к возникновению в общем случае отличной от нуля осредненной плотности турбулентного потока в некотором направлении, в то время как для составляющей скорости V_Т, согласно определению, должно быть V_Т≡0. Такой результат получается потому, что перенос тепла в заданном направлении обычно возникает в условиях наличия градиента теплосодержания вдоль этого направления. Это и приводит к тому, что в условиях равновероятного перемещения частиц воздуха в прямом и обратном направлениях результирующий поток получается не равным нулю и стремится уничтожить имеющийся градиент. В дальнейшем нас будут интересовать только средние значения турбулентной плотности потока тепла, для которых будем использовать прежнее обозначение.