Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 7

 Обычно горизонтальная составляющая средней скорости ветра в сотни раз превышает вертикальную. Соответственно, F_А – определяет перенос преимущественно в горизонтальном направлении и называется плотностью адвективного потока. Хотя, иногда и к вертикальной составляющей F_А применяют выражение «адвективный». Эти слабые вертикальные составляющие в ряде случаев играют важную роль в физике атмосферы.

Рассмотрим случай прямолинейного установившегося движения  вдоль оси x со средней скоростью[10] u(z) и попытаемся найти для этого случая выражение для средней плотности потока произвольной физической величины q в направлении z. Пока не будем связывать величину q  именно с теплом. Это может быть любая физическая величина. Учтем  неоднородность метеорологических элементов в воздушной массе. Разобьем ее на воздушные частицы, размеры которых выбраны так, что в пределах каждой из частиц метеорологические элементы постоянны.

Через горизонтальную площадку на высоте z за единицу времени проходит множество воздушных частиц, характеризующихся своим значением q_iρ_i  (предполагается, что q_i – некая физическая характеристика единицы массы воздуха, тогда произведение q_iρ_i  характеризует содержание физической величины в единице объема) и поперечным сечением S_i. Тогда средняя плотность потока вдоль оси z (величина потока через единичную площадку, ориентированную перпендикулярно рассматриваемому направлению, или, что то же самое, z-составляющая вектора плотности потока) может быть определена как

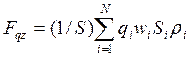                                         ,                                                                (15.2)

где

                                                  -

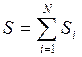сумма сечений всех N частиц, пересекших площадку за единицу времени. Здесь w_i – вертикальная составляющая скорости, - площадь горизонтального сечения i-й частицы в момент пересечения площадки. Эту же формулу можно записать как

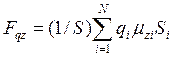                                           ,                                                                  (15.3)

где 

                                                  µ_i = ρ_iV_i                                                                                    (15.4)

– вектор количества движения частицы в расчете на единицу объема. Здесь суммирование ведется по всем воздушным частицам, пересекшим выбранную площадку за единицу времени. По условию задачи предполагается, что вертикальный  адвективный поток величины q, по смыслу равный произведению средних значений q и µ_z  всех частиц, отсутствует:                                                                                                

                                                 .

Это потому, что (адвективное движение в направлении вертикальной оси отсутствует в соответствии с условием рассматриваемой задачи). Здесь среднее значение произвольной величины a определяется согласно

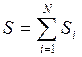                                         , .                                                       (15.5)

В общем случае, когда существует адвекция в вертикальном направлении, для определения вертикального турбулентного потока нужно взять разность:

                                        .                                                          (15.6)

В приведенных выше соотношениях закономерности турбулентного переноса не выражены явно.   Действительно, турбулентный поток записан через сумму по  существу  случайных величин.  Раскрыть закономерности призвана теория турбулентности. Достаточно много ученых занимались ее построением (Фридман, Келдыш, Колмогоров, Обухов, Ландау (СССР) и много зарубежных исследователей).

В частности, в 1931 г. Л.В. Келлеру удалось сформулировать условия, при которых для вертикального турбулентного потока величины q справедлива уже давно применявшаяся формула

                                         ,                                                                           (15.7)    

где k_z – коэффициент турбулентной вязкости в вертикальном направлении. Эти условия таковы: