Турбулентность. Особенности турбулентного движения, Тензор турбулентных напряжений. Конвективные, адвективные и турбулентные потоки физических величин, страница 4

Очевидно, что результаты будут зависеть от выбора масштаба усреднения. В частности, если выбранный масштаб превышает обычные размеры циклонов и антициклонов, мы должны получить нечто похожее на общую циркуляцию атмосферы[5]. А если в случае истечения из трубы выбрать достаточно большой масштаб осреднения, получим аналог стационарного течения.

Итак, мы хотим отказаться от детализации движения и перейти к рассмотрению осредненных характеристик движения. Однако на этом пути нас подстерегает неприятность, связанная с таким переходом.

Замечание по поводу осреднения. Если для всех неизвестных величин r, u, v, w, p, T  ввести средние одинаковым способом,  полученные характеристики не будут удовлетворять основным законам сохранения и уравнениям состояния, справедливым для истинных характеристик.

Действительно, пусть среднее значение величины определяется согласно , где  - мгновенные отклонения от среднего (или флуктуации). Очевидно, что по определению среднее значение  отклонения мгновенного значения  от его среднего  равно нулю. Проводя осреднение уравнения состояния и подставляя для флуктуирующих величин выражения, аналогичные приведенному выше, получим

                         .

Последний член в этом выражении, вообще говоря, может быть отличен от нуля, поскольку между флуктуациями температуры и плотности может быть связь[6]. Таким образом, уравнение состояния не выполняется для усредненных величин. Если мы стремимся сохранить это уравнение, то нужно для определения «среднего значения» давления    использовать другую процедуру:  чтобы выполнялось   должно быть , где , и среднее значение в отличие от , если .

В различных теориях турбулентности для определенного набора основных величин, например, p, r, rV,  осреднения вводятся некоторым одинаковым способом, а способы осреднения других величин определяются по соглашению так, чтобы удовлетворялись основные законы физики. При этом нужно еще позаботиться о методике экспериментального измерения таких “средних” величин, если мы намерены сравнивать теорию с экспериментом.

Осреднение уравнений движения

Теперь посмотрим, как можно выполнить процедуру осреднения в случае уравнений движения атмосферы. Представьте, что скорость может быть записана в виде суммы среднего значения за достаточно большой промежуток времени и отклонения от этого среднего (в духе предыдущего анализа):

                                     .        

По определению среднее значение . Нетрудно убедиться, что справедливы следующие соотношения[7]:

                 ,    ,   .

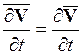Сначала рассмотрим уравнение неразрывности для плотности .  Часто полагают, что изменениями плотности можно пренебречь (это значит 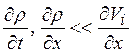 и т.п., то есть, скорость изменяется значительно быстрее, чем плотность).  Тогда получаем

                                                  , а .

В этом случае левую часть уравнения движения можно записать в виде

                             ,   ,

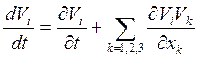или в векторной форме: 

                                          ,

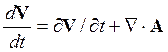где введен тензор с компонентами A_xy= uv, A_xx = u² и т.д., то есть,  A_ik = V_i V_k.   Убедитесь сами, что такая запись эквивалентна выражению , если .

Давайте посмотрим, что будет после усреднения тензора A?

                                ,

где

                               ,          .

Здесь учтено, что . Тогда

             ,

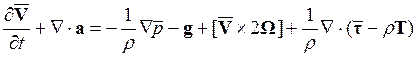Здесь r= const  считается.

По аналогии с тензором t величину rT называют тензором турбулентных напряжений.  Учитывая выражение для величин , можно сказать, что компоненты тензора турбулентных напряжений представляют собой ковариации флуктуаций компонент импульса единицы объема среды. Величина турбулентных напряжений, как средних характеристик движения, сильно зависит от конкретной задачи и масштаба осреднения. В частности, связь с масштабом осреднения очевидна, поскольку величина самих флуктуаций импульса зависит от этого масштаба. Подобные зависимости нужно устанавливать или постулировать на основании специальных гипотез или опытных данных (или рассчитывать на основании решения исходных неосредненных уравнений, что, как отмечалось, практически невозможно).